Integrator RNN Model

In this notebook, we train a vanilla RNN to integrate white noise. This example is useful on its own to understand how RNN training works.

import time
from functools import partial

import brainpy as bp
import brainpy.math.jax as bm

bp.math.use_backend('jax')

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.lines as mlines

Parameters

# Integration parameters
T = 1.0  # Arbitrary amount time, roughly physiological.
dt = 0.04
num_step = int(T / dt)  # Divide T into this many bins
bval = 0.01  # bias value limit
sval = 0.025  # standard deviation (before dividing by sqrt(dt))

# The scaling of the recurrent parameters in an RNN really matters.
# The correct scaling is 1/sqrt(number of recurrent inputs), which
# yields an order 1 signal output to a neuron if the input is order 1.
# Given that VRNN uses a tanh nonlinearity, with min and max output
# values of -1 and 1, this works out.  The scaling just below 1
# (0.95) is because we know we are making a line attractor so, we
# might as well start it off basically right 1.0 is also basically
# right, but perhaps will lead to crazier dynamics.
param_scale = 0.85  # Scaling of the recurrent weight matrix

# Optimization hyperparameters
l2reg = 0.0002  # amount of L2 regularization on the weights
num_train = 10000  # Total number of batches to train on.
num_batch = 128  # How many examples in each batch
max_grad_norm = 5.0  # Gradient clipping is HUGELY important for training RNNs
                     # max gradient norm before clipping, clip to this value.

Helpers

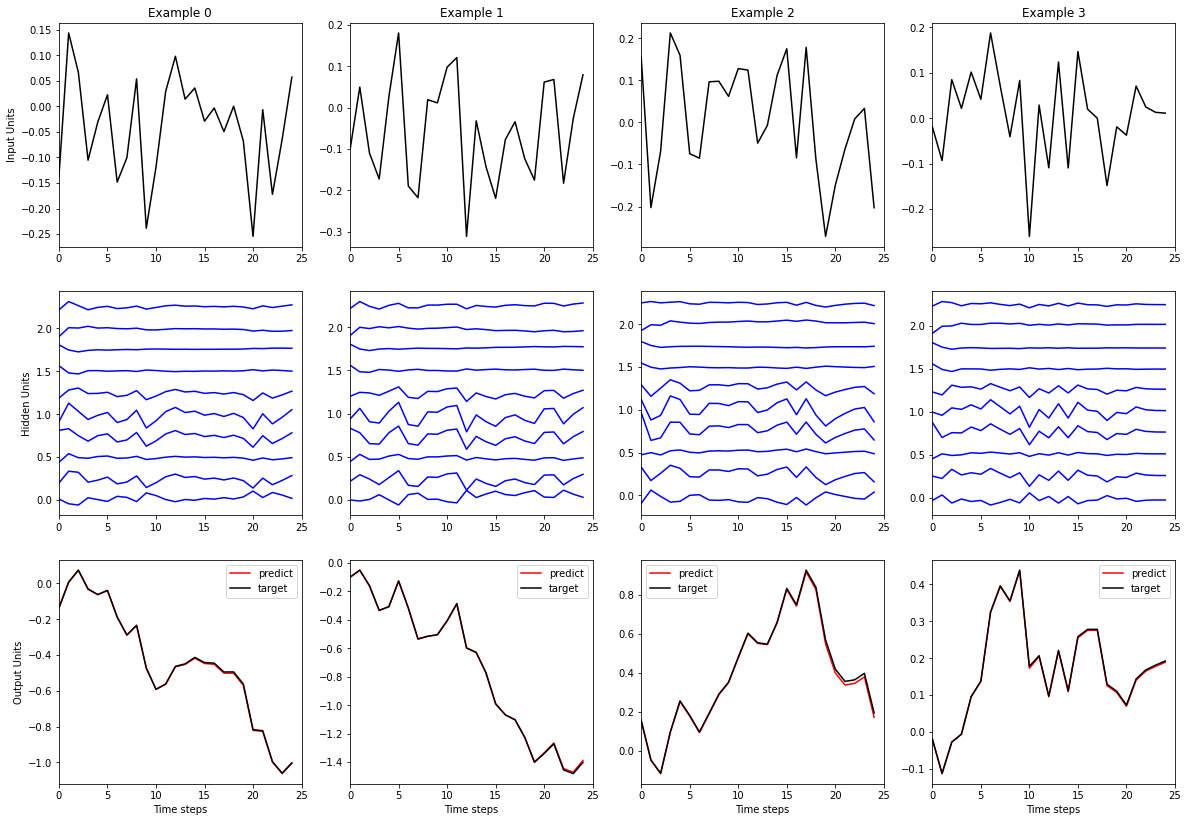
def plot_examples(num_time, inputs, hiddens, outputs, targets, num_example=1, num_plot=10):
  """Plot some input/hidden/output triplets."""
  plt.figure(figsize=(num_example * 5, 14))

  for bidx in range(num_example):
    plt.subplot(3, num_example, bidx + 1)
    plt.plot(inputs[:, bidx], 'k')
    plt.xlim([0, num_time])
    plt.title('Example %d' % bidx)
    if bidx == 0: plt.ylabel('Input Units')

  closeness = 0.25
  for bidx in range(num_example):
    plt.subplot(3, num_example, num_example + bidx + 1)
    plt.plot(hiddens[:, bidx, 0:num_plot] + closeness * np.arange(num_plot), 'b')
    plt.xlim([0, num_time])
    if bidx == 0: plt.ylabel('Hidden Units')

  for bidx in range(num_example):
    plt.subplot(3, num_example, 2 * num_example + bidx + 1)
    plt.plot(outputs[:, bidx, :], 'r', label='predict')
    plt.plot(targets[:, bidx, :], 'k', label='target')
    plt.xlim([0, num_time])
    plt.xlabel('Time steps')
    plt.legend()
    if bidx == 0: plt.ylabel('Output Units')

  plt.show()

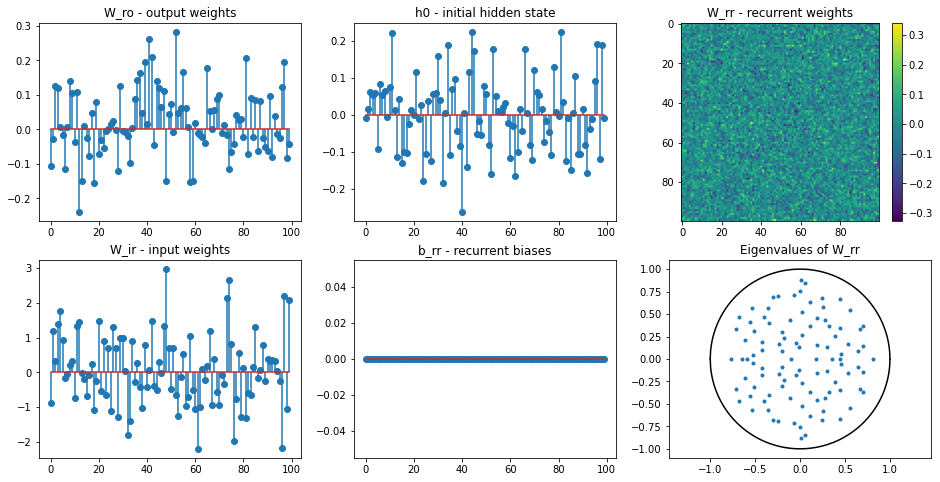
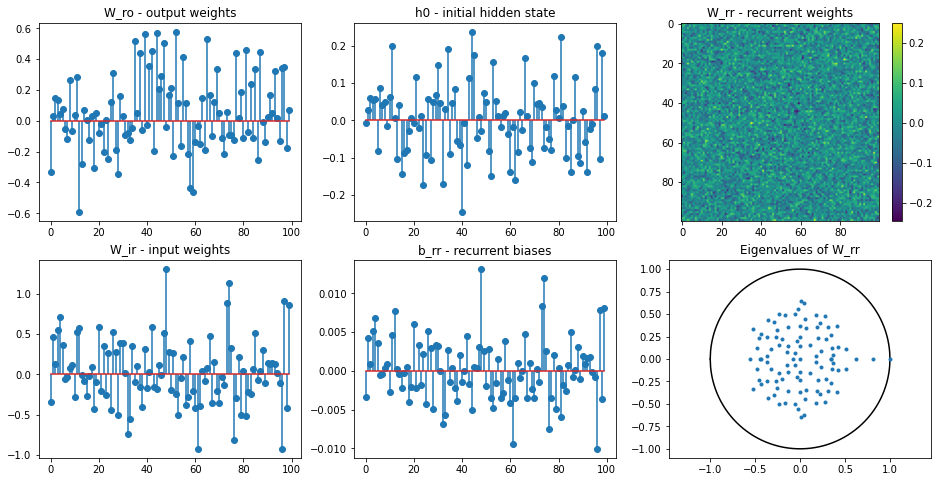
def plot_params(rnn):
  """ Plot the parameters of the vanilla RNN. """
  assert isinstance(rnn, IntegratorRNN)

  plt.figure(figsize=(16, 8))
  plt.subplot(231)
  plt.stem(rnn.w_ro.numpy()[:, 0])
  plt.title('W_ro - output weights')

  plt.subplot(232)
  plt.stem(rnn.h0)
  plt.title('h0 - initial hidden state')

  plt.subplot(233)
  plt.imshow(rnn.w_rr.numpy(), interpolation=None)
  plt.colorbar()
  plt.title('W_rr - recurrent weights')

  plt.subplot(234)
  plt.stem(rnn.w_ir.numpy()[0, :])
  plt.title('W_ir - input weights')

  plt.subplot(235)
  plt.stem(rnn.b_rr.numpy())
  plt.title('b_rr - recurrent biases')

  plt.subplot(236)
  evals, _ = np.linalg.eig(rnn.w_rr.numpy())
  x = np.linspace(-1, 1, 1000)
  plt.plot(x, np.sqrt(1 - x ** 2), 'k')
  plt.plot(x, -np.sqrt(1 - x ** 2), 'k')
  plt.plot(np.real(evals), np.imag(evals), '.')
  plt.axis('equal')
  plt.title('Eigenvalues of W_rr')

  plt.show()

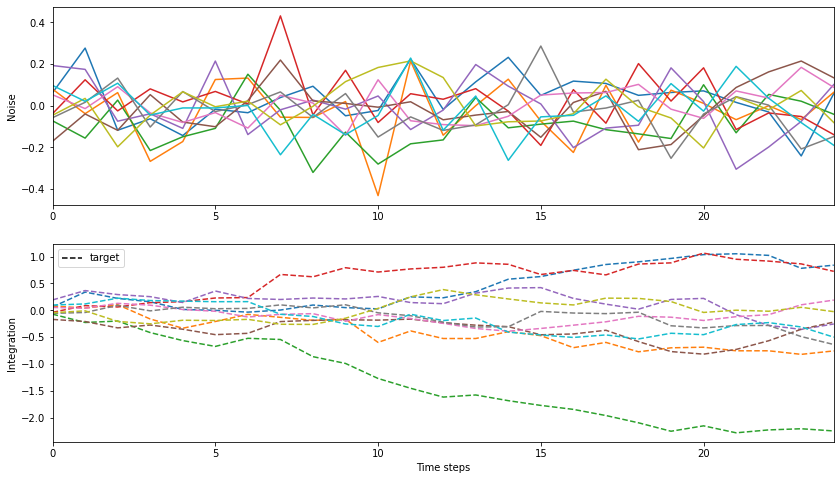
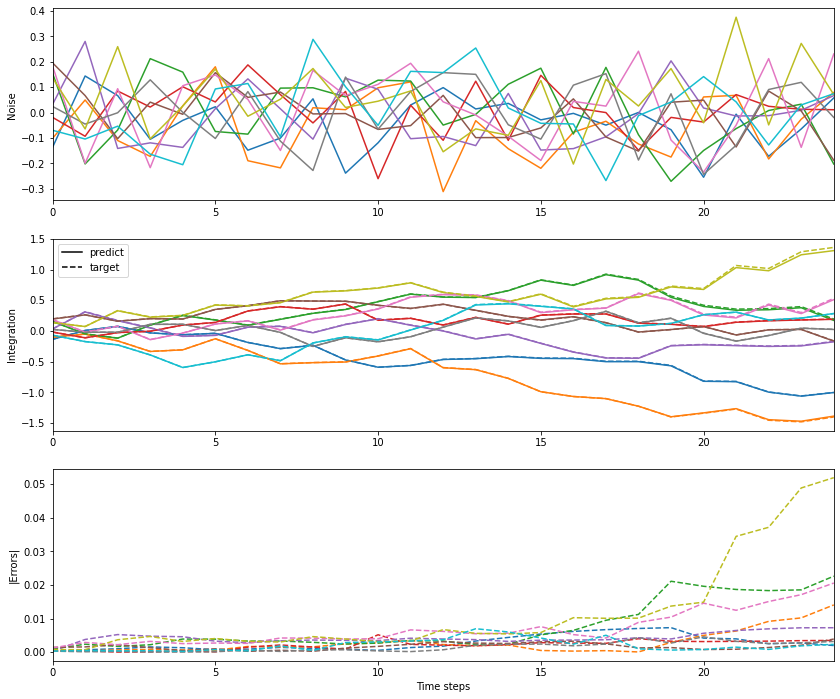
def plot_data(num_time, inputs, targets=None, outputs=None, errors=None, num_plot=10):
  """Plot some white noise / integrated white noise examples.

  Parameters
  ----------
  num_time : int
  num_plot : int
  inputs: ndarray
    with the shape of (num_batch, num_time, num_input)
  targets: ndarray
    with the shape of (num_batch, num_time, num_output)
  outputs: ndarray
    with the shape of (num_batch, num_time, num_output)
  errors: ndarray
    with the shape of (num_batch, num_time, num_output)
  """
  num = 1
  if errors is not None: num += 1
  if (targets is not None) or (outputs is not None): num += 1
  plt.figure(figsize=(14, 4 * num))

  # inputs
  plt.subplot(num, 1, 1)
  plt.plot(inputs[:, 0:num_plot, 0])
  plt.xlim([0, num_time - 1])
  plt.ylabel('Noise')

  legends = []
  if outputs is not None:
    plt.subplot(num, 1, 2)
    plt.plot(outputs[:, 0:num_plot, 0])
    plt.xlim([0, num_time - 1])
    legends.append(mlines.Line2D([], [], color='k', linestyle='-', label='predict'))
  if targets is not None:
    plt.subplot(num, 1, 2)
    plt.plot(targets[:, 0:num_plot, 0], '--')
    plt.xlim([0, num_time - 1])
    plt.ylabel("Integration")
    legends.append(mlines.Line2D([], [], color='k', linestyle='--', label='target'))
  if len(legends): plt.legend(handles=legends)

  if errors is not None:
    plt.subplot(num, 1, 3)
    plt.plot(errors[:, 0:num_plot, 0], '--')
    plt.xlim([0, num_time - 1])
    plt.ylabel("|Errors|")

  plt.xlabel('Time steps')
  plt.show()

@partial(bm.jit, dyn_vars=bp.TensorCollector({'a': bm.random.DEFAULT}))
def build_inputs_and_targets(mean, scale):
  """Build white noise input and integration targets."""

  # Create the white noise input.
  sample = bm.random.normal(size=(num_batch,))
  bias = mean * 2.0 * (sample - 0.5)
  samples = bm.random.normal(size=(num_step, num_batch))
  noise_t = scale / dt ** 0.5 * samples
  white_noise_t = bias + noise_t
  inputs_tx1 = bm.expand_dims(white_noise_t, axis=2)

  # * dt, intentionally left off to get output scaling in O(1).
  targets_tx1 = bm.expand_dims(bm.cumsum(white_noise_t, axis=0), axis=2)
  return inputs_tx1, targets_tx1

# Plot the example inputs and targets for the RNN.
_ints, _outs = build_inputs_and_targets(bval, sval)

plot_data(num_step, inputs=_ints, targets=_outs)

Models

class IntegratorRNN(bp.DynamicalSystem):
  target_backend = 'jax'

  def __init__(self, num_input, num_hidden, num_output, num_batch,
               g=1.0, l2_reg=2e-4, **kwargs):
    super(IntegratorRNN, self).__init__(**kwargs)

    # parameters
    self.num_input = num_input
    self.num_hidden = num_hidden
    self.num_output = num_output
    self.num_batch = num_batch
    self.g = g
    self.l2_reg = l2_reg
    self.rng = bm.random.RandomState()

    # weights
    self.w_ir = bm.TrainVar(self.rng.normal(scale=1 / num_input ** 0.5, size=(num_input, num_hidden)))
    self.w_rr = bm.TrainVar(self.rng.normal(scale=g / num_hidden ** 0.5, size=(num_hidden, num_hidden)))
    self.b_rr = bm.TrainVar(bm.zeros((num_hidden,)))
    self.w_ro = bm.TrainVar(self.rng.normal(scale=1 / num_hidden ** 0.5, size=(num_hidden, num_output)))
    self.b_ro = bm.TrainVar(bm.zeros((num_output,)))
    self.h0 = bm.TrainVar(self.rng.normal(scale=0.1, size=(num_hidden, )))

    # variables
    self.h = bm.Variable(bm.repeat(bm.expand_dims(self.h0, 0), self.num_batch, axis=0))
    self.o = bm.Variable(self.h @ self.w_ro)
    self.total_loss = bm.Variable(bm.zeros(1))
    self.l2_loss = bm.Variable(bm.zeros(1))
    self.mse_loss = bm.Variable(bm.zeros(1))

  def update(self, x, **kwargs):
    self.h.value = bm.tanh(self.h @ self.w_rr + x @ self.w_ir + self.b_rr)
    self.o.value = self.h @ self.w_ro + self.b_ro

  def predict(self, xs):
    self.h[:] = self.h0
    scan = bm.make_loop(self.update, dyn_vars=self.vars().unique(), out_vars=[self.h, self.o])
    return scan(xs)

  def loss(self, inputs, targets):
    _, predicts = self.predict(inputs)
    l2 = self.l2_reg * bm.losses.l2_norm([self.w_ir, self.w_rr, self.b_rr,
                                          self.w_ro, self.b_ro, self.h]) ** 2
    mse = bm.losses.mean_squared_error(predicts, targets)
    total = l2 + mse
    self.total_loss[0] = total
    self.l2_loss[0] = l2
    self.mse_loss[0] = mse
    return total

net = IntegratorRNN(num_input=1, num_hidden=100, num_output=1, num_batch=num_batch,
                    g=param_scale, l2_reg=l2reg)

plot_params(net)

lr = bm.optimizers.ExponentialDecay(lr=0.025, decay_steps=1, decay_rate=0.99975)
optimizer = bm.optimizers.Adam(lr=lr, train_vars=net.train_vars(), eps=1e-1)
grad_f = bm.grad(net.loss, dyn_vars=net.vars(), grad_vars=net.train_vars(), return_value=True)


@bm.jit
@bm.function(nodes=(net, optimizer))
def train(inputs, targets):
  grads, loss =grad_f(inputs, targets)
  clipped_grads = bm.clip_by_norm(grads, max_grad_norm)
  optimizer.update(clipped_grads)
  return loss

Training

t0 = time.time()
train_losses = {'total': [], 'l2': [], 'mse': []}
for i in range(num_train):
  _ins, _outs = build_inputs_and_targets(bval, sval)
  loss = train(inputs=_ins, targets=_outs)
  if (i + 1) % 100 == 0:
    print(f"Run batch {i} in {time.time() - t0:0.3f} s, learning rate: "
          f"{lr():.5f}, training loss {loss:0.4f}")

    train_losses['total'].append(net.total_loss[0])
    train_losses['l2'].append(net.l2_loss[0])
    train_losses['mse'].append(net.mse_loss[0])

Run batch 99 in 1.817 s, learning rate: 0.02438, training loss 0.1007
Run batch 199 in 2.464 s, learning rate: 0.02378, training loss 0.0957
Run batch 299 in 3.067 s, learning rate: 0.02319, training loss 0.0870
Run batch 399 in 3.678 s, learning rate: 0.02262, training loss 0.1056
Run batch 499 in 4.288 s, learning rate: 0.02206, training loss 0.0747
Run batch 599 in 4.882 s, learning rate: 0.02152, training loss 0.0738
Run batch 699 in 5.483 s, learning rate: 0.02099, training loss 0.0734
Run batch 799 in 6.074 s, learning rate: 0.02047, training loss 0.0761
Run batch 899 in 6.927 s, learning rate: 0.01996, training loss 0.0688
Run batch 999 in 7.521 s, learning rate: 0.01947, training loss 0.0723
Run batch 1099 in 8.111 s, learning rate: 0.01899, training loss 0.0773
Run batch 1199 in 8.699 s, learning rate: 0.01852, training loss 0.0713
Run batch 1299 in 9.286 s, learning rate: 0.01806, training loss 0.0637
Run batch 1399 in 9.873 s, learning rate: 0.01762, training loss 0.0583
Run batch 1499 in 10.456 s, learning rate: 0.01718, training loss 0.0561
Run batch 1599 in 11.041 s, learning rate: 0.01676, training loss 0.0584
Run batch 1699 in 11.626 s, learning rate: 0.01634, training loss 0.0569
Run batch 1799 in 12.215 s, learning rate: 0.01594, training loss 0.0875
Run batch 1899 in 12.803 s, learning rate: 0.01555, training loss 0.0484
Run batch 1999 in 13.386 s, learning rate: 0.01516, training loss 0.0713
Run batch 2099 in 13.969 s, learning rate: 0.01479, training loss 0.0487
Run batch 2199 in 14.551 s, learning rate: 0.01442, training loss 0.0512
Run batch 2299 in 15.139 s, learning rate: 0.01407, training loss 0.0526
Run batch 2399 in 15.718 s, learning rate: 0.01372, training loss 0.0523
Run batch 2499 in 16.308 s, learning rate: 0.01338, training loss 0.0517
Run batch 2599 in 16.935 s, learning rate: 0.01305, training loss 0.0539
Run batch 2699 in 17.518 s, learning rate: 0.01273, training loss 0.0440
Run batch 2799 in 18.101 s, learning rate: 0.01241, training loss 0.0457
Run batch 2899 in 18.686 s, learning rate: 0.01211, training loss 0.0614
Run batch 2999 in 19.269 s, learning rate: 0.01181, training loss 0.0395
Run batch 3099 in 19.852 s, learning rate: 0.01152, training loss 0.0401
Run batch 3199 in 20.438 s, learning rate: 0.01123, training loss 0.0398
Run batch 3299 in 21.025 s, learning rate: 0.01096, training loss 0.0411
Run batch 3399 in 21.608 s, learning rate: 0.01068, training loss 0.0384
Run batch 3499 in 22.189 s, learning rate: 0.01042, training loss 0.0390
Run batch 3599 in 22.773 s, learning rate: 0.01016, training loss 0.0458
Run batch 3699 in 23.356 s, learning rate: 0.00991, training loss 0.0358
Run batch 3799 in 23.936 s, learning rate: 0.00967, training loss 0.0386
Run batch 3899 in 24.518 s, learning rate: 0.00943, training loss 0.0358
Run batch 3999 in 25.102 s, learning rate: 0.00920, training loss 0.0324
Run batch 4099 in 25.685 s, learning rate: 0.00897, training loss 0.0340
Run batch 4199 in 26.269 s, learning rate: 0.00875, training loss 0.0390
Run batch 4299 in 26.849 s, learning rate: 0.00853, training loss 0.0308
Run batch 4399 in 27.429 s, learning rate: 0.00832, training loss 0.0345
Run batch 4499 in 28.012 s, learning rate: 0.00812, training loss 0.0312
Run batch 4599 in 28.595 s, learning rate: 0.00792, training loss 0.0328
Run batch 4699 in 29.178 s, learning rate: 0.00772, training loss 0.0298
Run batch 4799 in 29.761 s, learning rate: 0.00753, training loss 0.0333
Run batch 4899 in 30.347 s, learning rate: 0.00734, training loss 0.0316
Run batch 4999 in 30.929 s, learning rate: 0.00716, training loss 0.0305
Run batch 5099 in 31.516 s, learning rate: 0.00699, training loss 0.0295
Run batch 5199 in 32.100 s, learning rate: 0.00681, training loss 0.0296
Run batch 5299 in 32.680 s, learning rate: 0.00664, training loss 0.0273
Run batch 5399 in 33.267 s, learning rate: 0.00648, training loss 0.0306
Run batch 5499 in 33.865 s, learning rate: 0.00632, training loss 0.0290
Run batch 5599 in 34.453 s, learning rate: 0.00616, training loss 0.0299
Run batch 5699 in 35.038 s, learning rate: 0.00601, training loss 0.0281
Run batch 5799 in 35.622 s, learning rate: 0.00586, training loss 0.0294
Run batch 5899 in 36.209 s, learning rate: 0.00572, training loss 0.0264
Run batch 5999 in 36.791 s, learning rate: 0.00558, training loss 0.0288
Run batch 6099 in 37.376 s, learning rate: 0.00544, training loss 0.0278
Run batch 6199 in 37.959 s, learning rate: 0.00531, training loss 0.0258
Run batch 6299 in 38.542 s, learning rate: 0.00517, training loss 0.0233
Run batch 6399 in 39.127 s, learning rate: 0.00505, training loss 0.0257
Run batch 6499 in 39.709 s, learning rate: 0.00492, training loss 0.0258
Run batch 6599 in 40.295 s, learning rate: 0.00480, training loss 0.0260
Run batch 6699 in 40.881 s, learning rate: 0.00468, training loss 0.0262
Run batch 6799 in 41.475 s, learning rate: 0.00457, training loss 0.0258
Run batch 6899 in 42.060 s, learning rate: 0.00445, training loss 0.0250
Run batch 6999 in 42.641 s, learning rate: 0.00434, training loss 0.0244
Run batch 7099 in 43.227 s, learning rate: 0.00424, training loss 0.0237
Run batch 7199 in 43.812 s, learning rate: 0.00413, training loss 0.0244
Run batch 7299 in 44.394 s, learning rate: 0.00403, training loss 0.0236
Run batch 7399 in 44.976 s, learning rate: 0.00393, training loss 0.0261
Run batch 7499 in 45.560 s, learning rate: 0.00383, training loss 0.0226
Run batch 7599 in 46.141 s, learning rate: 0.00374, training loss 0.0240
Run batch 7699 in 46.721 s, learning rate: 0.00365, training loss 0.0242
Run batch 7799 in 47.303 s, learning rate: 0.00356, training loss 0.0229
Run batch 7899 in 47.885 s, learning rate: 0.00347, training loss 0.0237
Run batch 7999 in 48.466 s, learning rate: 0.00338, training loss 0.0245
Run batch 8099 in 49.049 s, learning rate: 0.00330, training loss 0.0243
Run batch 8199 in 49.629 s, learning rate: 0.00322, training loss 0.0235
Run batch 8299 in 50.212 s, learning rate: 0.00314, training loss 0.0243
Run batch 8399 in 50.798 s, learning rate: 0.00306, training loss 0.0225
Run batch 8499 in 51.378 s, learning rate: 0.00299, training loss 0.0228
Run batch 8599 in 51.963 s, learning rate: 0.00291, training loss 0.0247
Run batch 8699 in 52.548 s, learning rate: 0.00284, training loss 0.0239
Run batch 8799 in 53.133 s, learning rate: 0.00277, training loss 0.0223
Run batch 8899 in 53.717 s, learning rate: 0.00270, training loss 0.0227
Run batch 8999 in 54.296 s, learning rate: 0.00263, training loss 0.0230
Run batch 9099 in 54.878 s, learning rate: 0.00257, training loss 0.0257
Run batch 9199 in 55.456 s, learning rate: 0.00251, training loss 0.0231
Run batch 9299 in 56.038 s, learning rate: 0.00244, training loss 0.0232
Run batch 9399 in 56.620 s, learning rate: 0.00238, training loss 0.0238
Run batch 9499 in 57.205 s, learning rate: 0.00233, training loss 0.0224
Run batch 9599 in 57.790 s, learning rate: 0.00227, training loss 0.0220
Run batch 9699 in 58.372 s, learning rate: 0.00221, training loss 0.0218
Run batch 9799 in 58.954 s, learning rate: 0.00216, training loss 0.0233
Run batch 9899 in 59.535 s, learning rate: 0.00210, training loss 0.0212
Run batch 9999 in 60.117 s, learning rate: 0.00205, training loss 0.0212

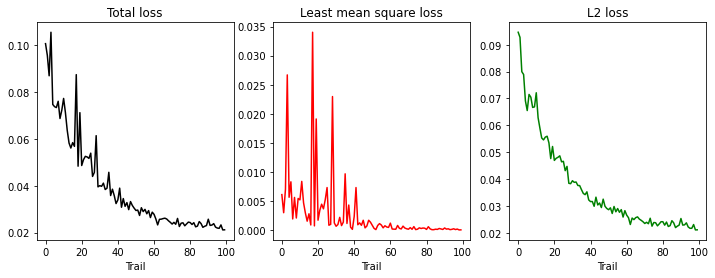
# Show the loss through training.
plt.figure(figsize=(12, 4))
plt.subplot(131)
plt.plot(train_losses['total'], 'k')
plt.title('Total loss')
plt.xlabel('Trail')

plt.subplot(132)
plt.plot(train_losses['mse'], 'r')
plt.title('Least mean square loss')
plt.xlabel('Trail')

plt.subplot(133)
plt.plot(train_losses['l2'], 'g')
plt.title('L2 loss')
plt.xlabel('Trail')
plt.show()

# Show the trained weights
plot_params(net)

Testing

inputs, hiddens, outputs, targets = [], [], [], []
for n in range(16):
  input_b, target_b = build_inputs_and_targets(bval, sval)
  h_b, o_b = net.predict(input_b)
  inputs.append(input_b)
  hiddens.append(h_b)
  outputs.append(o_b)
  targets.append(target_b)
inputs = np.hstack(inputs)
hiddens = np.hstack(hiddens)
outputs = np.hstack(outputs)
targets = np.hstack(targets)

plot_data(num_step, inputs=inputs, targets=targets, outputs=outputs, errors=np.abs(targets - outputs))

plot_examples(num_step, inputs=inputs, targets=targets, outputs=outputs, hiddens=hiddens, num_example=4)