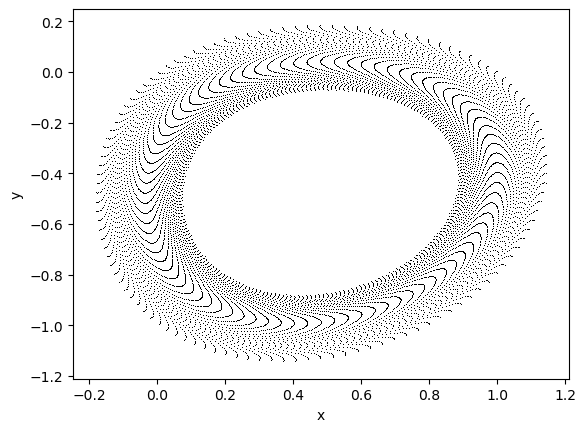
Hénon map
The Hénon map is a discrete-time dynamical system. It is one of the most studied examples of dynamical systems that exhibit chaotic behavior. The Hénon map takes a point \((x_n, y_n)\) in the plane and maps it to a new point
\[\begin{split}\begin{cases}x_{n+1} = 1-a x_n^2 + y_n\\y_{n+1} = b x_n.\end{cases}\end{split}\]
[1]:
import brainpy as bp
import brainpy.math as bm
import matplotlib.pyplot as plt
[2]:
class HenonMap(bp.dyn.DynamicalSystem):
"""Hénon map."""
def __init__(self, num, a=1.4, b=0.3):
super(HenonMap, self).__init__()
# parameters
self.a = a
self.b = b
self.num = num
# variables
self.x = bm.Variable(bm.zeros(num))
self.y = bm.Variable(bm.zeros(num))
def update(self, _t, _dt):
x_new = 1 - self.a * self.x * self.x + self.y
self.y.value = self.b * self.x
self.x.value = x_new
[3]:
map = HenonMap(4)
map.a = bm.asarray([0.5, 1.0, 1.4, 2.0])
WARNING:absl:No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.)
[4]:
runner = bp.dyn.DSRunner(map, monitors=['x', 'y'], dt=1)
runner.run(10000)
[4]:
0.3052709102630615
[5]:
fig, gs = bp.visualize.get_figure(4, 1, 4, 6)
for i in range(map.num):
fig.add_subplot(gs[i, 0])
plt.plot(runner.mon.x[:, i], runner.mon.y[:, i], '.k')
plt.xlabel('x')
plt.ylabel('y')
plt.title(f'a={map.a[i]}')
if (i + 1) == map.num:
plt.show()
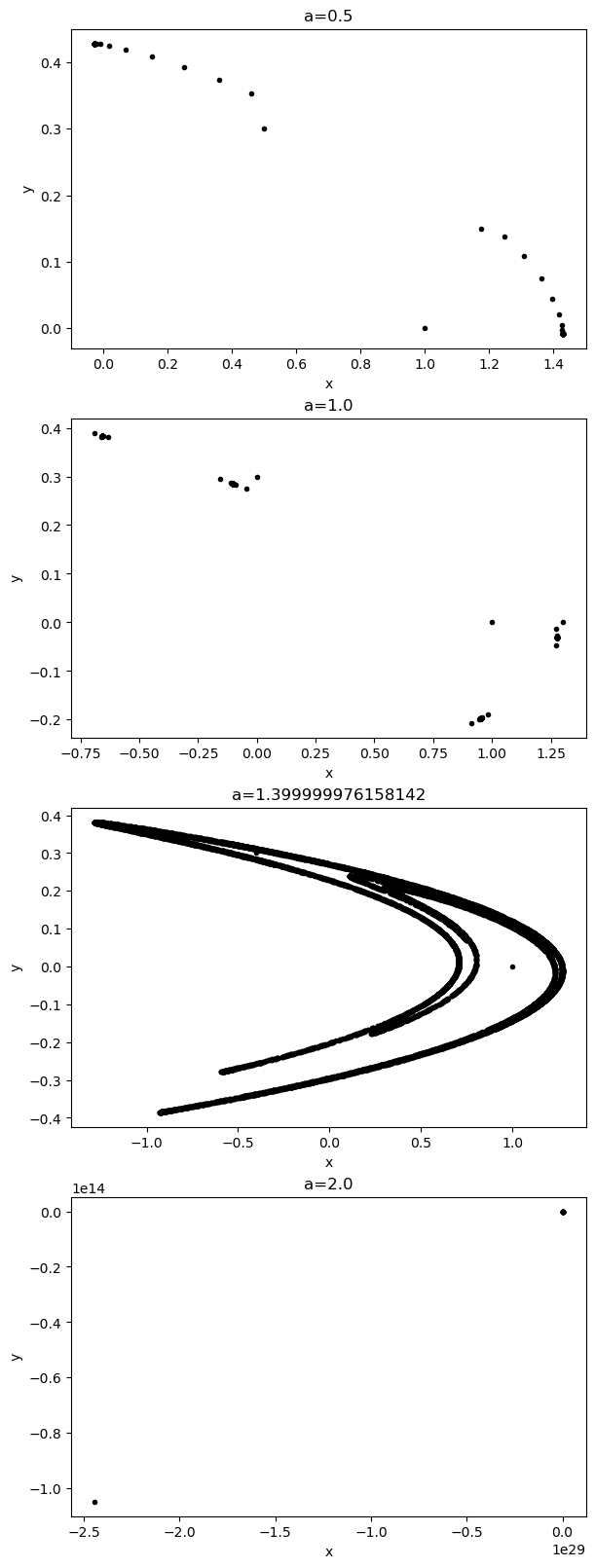
The strange attractor illustrated above is obtained for \(a=1.4\) and \(b=0.3\).
[6]:
map = HenonMap(1)
map.a = 0.2
map.b = 0.9991
runner = bp.dyn.DSRunner(map, monitors=['x', 'y'], dt=1)
runner.run(10000)
plt.plot(runner.mon.x[:, 0], runner.mon.y[:, 0], ',k')
plt.xlabel('x')
plt.ylabel('y')
plt.xlim([-5, 5])
plt.ylim([-5, 5])
plt.show()
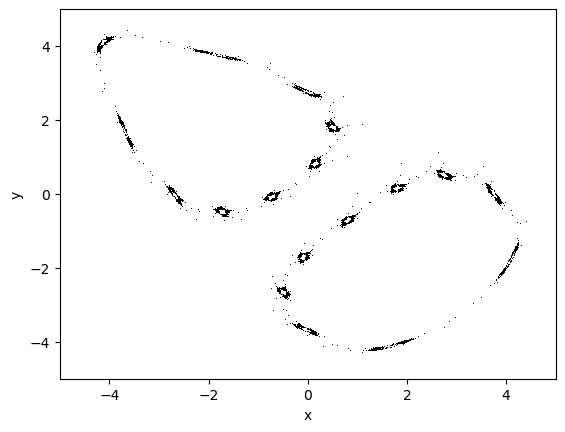
[7]:
map = HenonMap(1)
map.a = 0.2
map.b = -0.9999
runner = bp.dyn.DSRunner(map, monitors=['x', 'y'], dt=1)
runner.run(10000)
plt.plot(runner.mon.x[:, 0], runner.mon.y[:, 0], ',k')
plt.xlabel('x')
plt.ylabel('y')
plt.show()