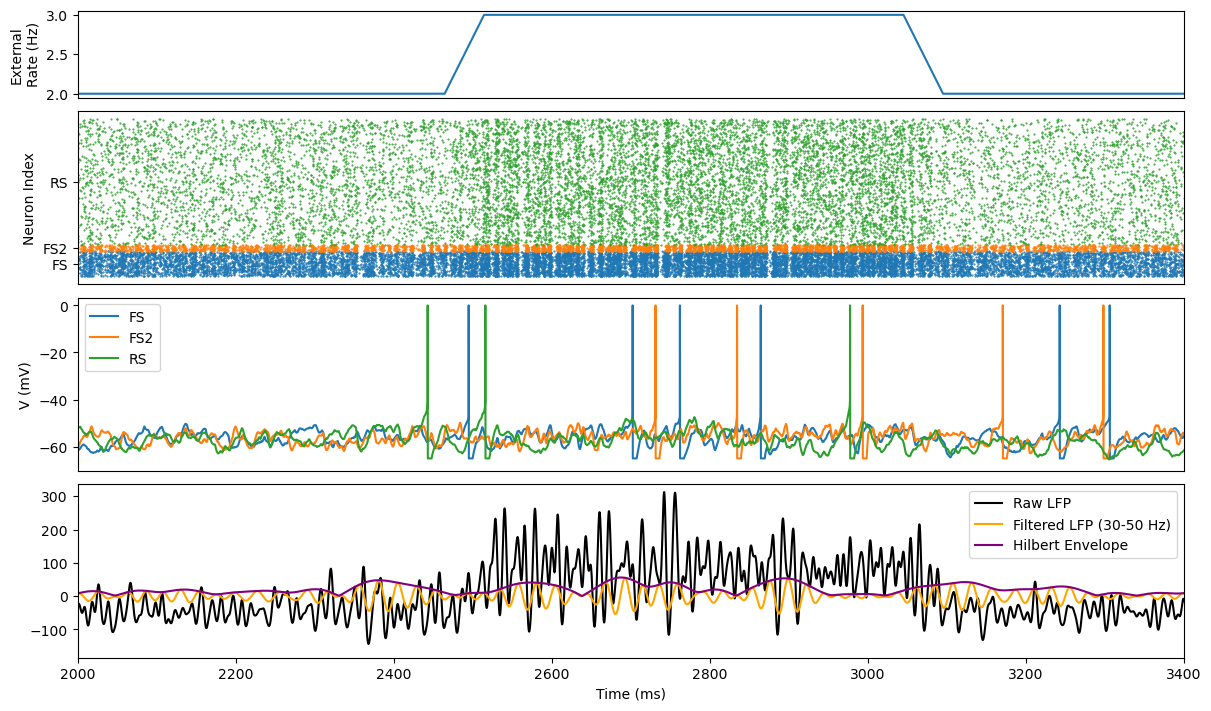
(Susin & Destexhe, 2021): ING Network for Generating Gamma Oscillation
Implementation of the paper:
Susin, Eduarda, and Alain Destexhe. “Integration, coincidence detection and resonance in networks of spiking neurons expressing gamma oscillations and asynchronous states.” PLoS computational biology 17.9 (2021): e1009416.
[1]:
import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import kaiserord, lfilter, firwin, hilbert
import brainpy as bp
import brainpy.math as bm
[2]:
# Table 1: specific neuron model parameters
RS_par = dict(Vth=-40, delta=2., tau_ref=5., tau_w=500, a=4, b=20, C=150, gL=10, EL=-65, V_reset=-65,
E_e=0., E_i=-80.)
FS_par = dict(Vth=-47.5, delta=0.5, tau_ref=5., tau_w=500, a=0, b=0, C=150, gL=10, EL=-65, V_reset=-65,
E_e=0., E_i=-80.)
Ch_par = dict(Vth=-47.5, delta=0.5, tau_ref=1., tau_w=50, a=80, b=150, C=150, gL=10, EL=-58, V_reset=-65,
E_e=0., E_i=-80.)
[3]:
class AdEx(bp.NeuGroup):
def __init__(
self,
size,
# neuronal parameters
Vth=-40, delta=2., tau_ref=5., tau_w=500, a=4, b=20, C=150,
gL=10, EL=-65, V_reset=-65, V_sp_th=-30.,
# synaptic parameters
tau_e=1.5, tau_i=7.5, E_e=0., E_i=-80.,
# other parameters
name=None, method='exp_euler',
V_initializer=bp.init.Uniform(-65, -50),
w_initializer=bp.init.Constant(0.),
):
super(AdEx, self).__init__(size=size, name=name)
# neuronal parameters
self.Vth = Vth
self.delta = delta
self.tau_ref = tau_ref
self.tau_w = tau_w
self.a = a
self.b = b
self.C = C
self.gL = gL
self.EL = EL
self.V_reset = V_reset
self.V_sp_th = V_sp_th
# synaptic parameters
self.tau_e = tau_e
self.tau_i = tau_i
self.E_e = E_e
self.E_i = E_i
# neuronal variables
self.V = bp.init.variable_(V_initializer, self.num)
self.w = bp.init.variable_(w_initializer, self.num)
self.spike = bm.Variable(self.num, dtype=bool)
self.refractory = bm.Variable(self.num, dtype=bool)
self.t_last_spike = bm.Variable(bm.ones(self.num) * -1e8)
# synaptic parameters
self.ge = bm.Variable(self.num)
self.gi = bm.Variable(self.num)
# integral
self.integral = bp.odeint(bp.JointEq(self.dV, self.dw, self.dge, self.dgi), method=method)
def dge(self, ge, t):
return -ge / self.tau_e
def dgi(self, gi, t):
return -gi / self.tau_i
def dV(self, V, t, w, ge, gi, Iext=None):
I = ge * (self.E_e - V) + gi * (self.E_i - V)
if Iext is not None: I += Iext
dVdt = (self.gL * self.delta * bm.exp((V - self.Vth) / self.delta)
- w + self.gL * (self.EL - V) + I) / self.C
return dVdt
def dw(self, w, t, V):
dwdt = (self.a * (V - self.EL) - w) / self.tau_w
return dwdt
def update(self, tdi, x=None):
V, w, ge, gi = self.integral(self.V.value, self.w.value, self.ge.value, self.gi.value,
tdi.t, Iext=x, dt=tdi.dt)
refractory = (tdi.t - self.t_last_spike) <= self.tau_ref
V = bm.where(refractory, self.V.value, V)
spike = V >= self.V_sp_th
self.V.value = bm.where(spike, self.V_reset, V)
self.w.value = bm.where(spike, w + self.b, w)
self.ge.value = ge
self.gi.value = gi
self.spike.value = spike
self.refractory.value = bm.logical_or(refractory, spike)
self.t_last_spike.value = bm.where(spike, tdi.t, self.t_last_spike)
[4]:
class INGNet(bp.Network):
def __init__(self, ext_varied_rates, ext_weight=0.9, method='exp_euler', dt=bm.get_dt()):
super(INGNet, self).__init__()
self.num_rs = 20000
self.num_fs = 4000
self.num_fs2 = 1000
self.exc_syn_tau = 5. # ms
self.inh_syn_tau = 5. # ms
self.exc_syn_weight = 1. # nS
self.inh_syn_weight = 5. # nS
self.num_delay_step = int(1.5 / dt)
self.ext_varied_rates = ext_varied_rates
# neuronal populations
RS_par_ = RS_par.copy()
FS_par_ = FS_par.copy()
FS2_par_ = FS_par.copy()
RS_par_.update(Vth=-50, V_sp_th=-40)
FS_par_.update(Vth=-50, V_sp_th=-40)
FS2_par_.update(Vth=-50, V_sp_th=-40)
self.rs_pop = AdEx(self.num_rs, tau_e=self.exc_syn_tau, tau_i=self.inh_syn_tau, method=method, **RS_par_)
self.fs_pop = AdEx(self.num_fs, tau_e=self.exc_syn_tau, tau_i=self.inh_syn_tau, method=method, **FS_par_)
self.fs2_pop = AdEx(self.num_fs2, tau_e=self.exc_syn_tau, tau_i=self.inh_syn_tau, method=method, **FS2_par_)
self.ext_pop = bp.neurons.PoissonGroup(self.num_rs, freqs=bm.Variable(1))
# Poisson inputs
self.ext_to_FS = bp.synapses.Delta(self.ext_pop, self.fs_pop, bp.conn.FixedProb(0.02),
output=bp.synouts.CUBA(target_var='ge'),
g_max=ext_weight)
self.ext_to_RS = bp.synapses.Delta(self.ext_pop, self.rs_pop, bp.conn.FixedProb(0.02),
output=bp.synouts.CUBA(target_var='ge'),
g_max=ext_weight)
self.ext_to_FS2 = bp.synapses.Delta(self.ext_pop, self.fs2_pop, bp.conn.FixedProb(0.02),
output=bp.synouts.CUBA(target_var='ge'),
g_max=ext_weight)
# synaptic projections
self.RS_to_FS = bp.synapses.Delta(self.rs_pop, self.fs_pop, bp.conn.FixedProb(0.02),
output=bp.synouts.CUBA(target_var='ge'),
g_max=self.exc_syn_weight,
delay_step=self.num_delay_step)
self.RS_to_RS = bp.synapses.Delta(self.rs_pop, self.rs_pop, bp.conn.FixedProb(0.02),
output=bp.synouts.CUBA(target_var='ge'),
g_max=self.exc_syn_weight,
delay_step=self.num_delay_step)
self.RS_to_FS2 = bp.synapses.Delta(self.rs_pop, self.fs2_pop, bp.conn.FixedProb(0.15),
output=bp.synouts.CUBA(target_var='ge'),
g_max=self.exc_syn_weight,
delay_step=self.num_delay_step)
self.FS_to_RS = bp.synapses.Delta(self.fs_pop, self.rs_pop, bp.conn.FixedProb(0.02),
output=bp.synouts.CUBA(target_var='gi'),
g_max=self.inh_syn_weight,
delay_step=self.num_delay_step)
self.FS_to_FS = bp.synapses.Delta(self.fs_pop, self.fs_pop, bp.conn.FixedProb(0.02),
output=bp.synouts.CUBA(target_var='gi'),
g_max=self.inh_syn_weight,
delay_step=self.num_delay_step)
self.FS_to_FS2 = bp.synapses.Delta(self.fs_pop, self.fs2_pop, bp.conn.FixedProb(0.03),
output=bp.synouts.CUBA(target_var='gi'),
g_max=self.inh_syn_weight,
delay_step=self.num_delay_step)
self.FS2_to_RS = bp.synapses.Delta(self.fs2_pop, self.rs_pop, bp.conn.FixedProb(0.15),
output=bp.synouts.CUBA(target_var='gi'),
g_max=self.exc_syn_weight,
delay_step=self.num_delay_step)
self.FS2_to_FS = bp.synapses.Delta(self.fs2_pop, self.fs_pop, bp.conn.FixedProb(0.15),
output=bp.synouts.CUBA(target_var='gi'),
g_max=self.exc_syn_weight,
delay_step=self.num_delay_step)
self.FS2_to_FS2 = bp.synapses.Delta(self.fs2_pop, self.fs2_pop, bp.conn.FixedProb(0.6),
output=bp.synouts.CUBA(target_var='gi'),
g_max=self.exc_syn_weight,
delay_step=self.num_delay_step)
def change_freq(self, tdi):
self.ext_pop.freqs[0] = self.ext_varied_rates[tdi.i]
[5]:
def get_inputs(c_low, c_high, t_transition, t_min_plato, t_max_plato, t_gap, t_total, dt=None):
dt = bm.get_dt() if dt is None else dt
t = 0
num_gap = int(t_gap / dt)
num_total = int(t_total / dt)
num_transition = int(t_transition / dt)
inputs = []
ramp_up = np.linspace(c_low, c_high, num_transition)
ramp_down = np.linspace(c_high, c_low, num_transition)
plato_base = np.ones(num_gap) * c_low
while t < num_total:
num_plato = int(np.random.uniform(low=t_min_plato, high=t_max_plato, size=1) / dt)
inputs.extend([plato_base, ramp_up, np.ones(num_plato) * c_high, ramp_down])
t += (num_gap + num_transition + num_plato + num_transition)
return bm.asarray(np.concatenate(inputs)[:num_total])
[6]:
def signal_phase_by_Hilbert(signal, signal_time, low_cut, high_cut, sampling_space):
# sampling_space: in seconds (no units)
# signal_time: in seconds (no units)
# low_cut: in Hz (no units)(band to filter)
# high_cut: in Hz (no units)(band to filter)
signal = signal - np.mean(signal)
width = 5.0 # The desired width in Hz of the transition from pass to stop
ripple_db = 60.0 # The desired attenuation in the stop band, in dB.
sampling_rate = 1. / sampling_space
Nyquist = sampling_rate / 2.
num_taps, beta = kaiserord(ripple_db, width / Nyquist)
if num_taps % 2 == 0:
num_taps = num_taps + 1 # Numtaps must be odd
taps = firwin(num_taps, [low_cut / Nyquist, high_cut / Nyquist], window=('kaiser', beta), nyq=1.0,
pass_zero=False, scale=True)
filtered_signal = lfilter(taps, 1.0, signal)
delay = 0.5 * (num_taps - 1) / sampling_rate # To corrected to zero-phase
delay_index = int(np.floor(delay * sampling_rate))
filtered_signal = filtered_signal[num_taps - 1:] # taking out the "corrupted" signal
# correcting the delay and taking out the "corrupted" signal part
filtered_time = signal_time[num_taps - 1:] - delay
cutted_signal = signal[(num_taps - 1 - delay_index): (len(signal) - (num_taps - 1 - delay_index))]
# --------------------------------------------------------------------------
# The hilbert transform are very slow when the signal has odd lenght,
# This part check if the length is odd, and if this is the case it adds a zero in the end
# of all the vectors related to the filtered Signal:
if len(filtered_signal) % 2 != 0: # If the lengh is odd
tmp1 = filtered_signal.tolist()
tmp1.append(0)
tmp2 = filtered_time.tolist()
tmp2.append((len(filtered_time) + 1) * sampling_space + filtered_time[0])
tmp3 = cutted_signal.tolist()
tmp3.append(0)
filtered_signal = np.asarray(tmp1)
filtered_time = np.asarray(tmp2)
cutted_signal = np.asarray(tmp3)
# --------------------------------------------------------------------------
ht_filtered_signal = hilbert(filtered_signal)
envelope = np.abs(ht_filtered_signal)
phase = np.angle(ht_filtered_signal) # The phase is between -pi and pi in radians
return filtered_time, filtered_signal, cutted_signal, envelope, phase
[7]:
def visualize_simulation_results(times, spikes, example_potentials, varied_rates,
xlim=None, t_lfp_start=None, t_lfp_end=None, filename=None):
fig, gs = bp.visualize.get_figure(7, 1, 1, 12)
# 1. input firing rate
ax = fig.add_subplot(gs[0])
plt.plot(times, varied_rates)
if xlim is None:
xlim = (0, times[-1])
ax.set_xlim(*xlim)
ax.set_xticks([])
ax.set_ylabel('External\nRate (Hz)')
# 2. inhibitory cell rater plot
ax = fig.add_subplot(gs[1: 3])
i = 0
y_ticks = ([], [])
for key, (sp_matrix, sp_type) in spikes.items():
iis, sps = np.where(sp_matrix)
tts = times[iis]
plt.plot(tts, sps + i, '.', markersize=1, label=key)
y_ticks[0].append(i + sp_matrix.shape[1] / 2)
y_ticks[1].append(key)
i += sp_matrix.shape[1]
ax.set_xlim(*xlim)
ax.set_xlabel('')
ax.set_ylabel('Neuron Index')
ax.set_xticks([])
ax.set_yticks(*y_ticks)
# ax.legend()
# 3. example membrane potential
ax = fig.add_subplot(gs[3: 5])
for key, potential in example_potentials.items():
vs = np.where(spikes[key][0][:, 0], 0, potential)
plt.plot(times, vs, label=key)
ax.set_xlim(*xlim)
ax.set_xticks([])
ax.set_ylabel('V (mV)')
ax.legend()
# 4. LFP
ax = fig.add_subplot(gs[5:7])
ax.set_xlim(*xlim)
t1 = int(t_lfp_start / bm.get_dt()) if t_lfp_start is not None else 0
t2 = int(t_lfp_end / bm.get_dt()) if t_lfp_end is not None else len(times)
times = times[t1: t2]
lfp = 0
for sp_matrix, sp_type in spikes.values():
lfp += bp.measure.unitary_LFP(times, sp_matrix[t1: t2], sp_type)
phase_ts, filtered, cutted, envelope, _ = signal_phase_by_Hilbert(bm.as_numpy(lfp), times * 1e-3, 30, 50,
bm.get_dt() * 1e-3)
plt.plot(phase_ts * 1e3, cutted, color='k', label='Raw LFP')
plt.plot(phase_ts * 1e3, filtered, color='orange', label="Filtered LFP (30-50 Hz)")
plt.plot(phase_ts * 1e3, envelope, color='purple', label="Hilbert Envelope")
plt.legend(loc='best')
plt.xlabel('Time (ms)')
# save or show
if filename:
plt.savefig(filename, dpi=500)
plt.show()
[8]:
def simulate_ing_net():
duration = 6e3
varied_rates = get_inputs(2., 3., 50., 350, 600, 1e3, duration)
net = INGNet(varied_rates, ext_weight=0.9)
runner = bp.DSRunner(
net,
inputs=net.change_freq,
monitors={'FS.V0': lambda tdi: net.fs_pop.V[0],
'FS2.V0': lambda tdi: net.fs2_pop.V[0],
'RS.V0': lambda tdi: net.rs_pop.V[0],
'FS.spike': lambda tdi: net.fs_pop.spike,
'FS2.spike': lambda tdi: net.fs2_pop.spike,
'RS.spike': lambda tdi: net.rs_pop.spike}
)
runner.run(duration)
visualize_simulation_results(times=runner.mon.ts,
spikes={'FS': (runner.mon['FS.spike'], 'inh'),
'FS2': (runner.mon['FS2.spike'], 'inh'),
'RS': (runner.mon['RS.spike'], 'exc')},
example_potentials={'FS': runner.mon['FS.V0'],
'FS2': runner.mon['FS2.V0'],
'RS': runner.mon['RS.V0']},
varied_rates=varied_rates.to_numpy(),
xlim=(2e3, 3.4e3), t_lfp_start=1e3, t_lfp_end=5e3)
[9]:
simulate_ing_net()
WARNING:jax._src.lib.xla_bridge:No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.)