Multiscroll chaotic attractor (多卷波混沌吸引子)
Multiscroll attractors also called n-scroll attractor include the Chen attractor, the Lu Chen attractor, the modified Chen chaotic attractor, PWL Duffing attractor, Rabinovich Fabrikant attractor, modified Chua chaotic attractor, that is, multiple scrolls in a single attractor.
[1]:
import brainpy as bp
import brainpy.math as bm
import matplotlib.pyplot as plt
[2]:
bp.__version__
[2]:
'2.4.3'
[3]:
def run_and_visualize(runner, duration=100, dim=3, args=None):
assert dim in [3, 2]
if args is None:
runner.run(duration)
else:
runner.run(duration, args=args)
if dim == 3:
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
for i in range(runner.mon.x.shape[1]):
plt.plot(runner.mon.x[100:, i], runner.mon.y[100:, i], runner.mon.z[100:, i])
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
else:
for i in range(runner.mon.x.shape[1]):
plt.plot(runner.mon.x[100:, i], runner.mon.y[100:, i])
plt.xlabel('x')
plt.xlabel('y')
plt.show()
Chen attractor
The Chen system is defined as follows [1]
[4]:
@bp.odeint(method='euler')
def chen_system(x, y, z, t, a=40, b=3, c=28):
dx = a * (y - x)
dy = (c - a) * x - x * z + c * y
dz = x * y - b * z
return dx, dy, dz
[5]:
runner = bp.IntegratorRunner(
chen_system,
monitors=['x', 'y', 'z'],
inits=dict(x=-0.1, y=0.5, z=-0.6),
dt=0.001
)
run_and_visualize(runner, 100)
No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.)
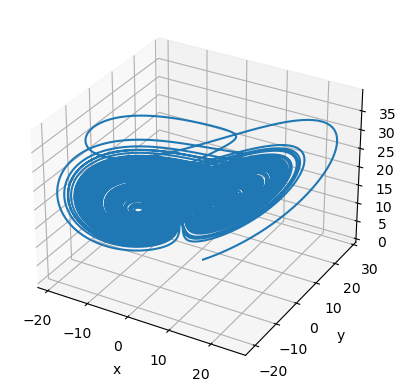
Lu Chen attractor
An extended Chen system with multiscroll was proposed by Jinhu Lu (吕金虎) and Guanrong Chen [2].
当 u ≤-11 时,Lṻ Chen 混沌吸引子为左卷波混沌吸引子,
当u 在 -10 和 10 之间 时为麻花型吸引子,
当 u≥ 11 ,是右卷波混沌吸引子。
[6]:
@bp.odeint(method='rk4')
def lu_chen_system(x, y, z, t, a=36, c=20, b=3, u=-15.15):
dx = a * (y - x)
dy = x - x * z + c * y + u
dz = x * y - b * z
return dx, dy, dz
[7]:
runner = bp.IntegratorRunner(
lu_chen_system,
monitors=['x', 'y', 'z'],
inits=dict(x=0.1, y=0.3, z=-0.6),
dt=0.002
)
run_and_visualize(runner, 100, args=dict(u=-15.15),)
runner = bp.IntegratorRunner(
lu_chen_system,
monitors=['x', 'y', 'z'],
inits=dict(x=0.1, y=0.3, z=-0.6),
dt=0.002
)
run_and_visualize(runner, 100, args=dict(u=-8),)
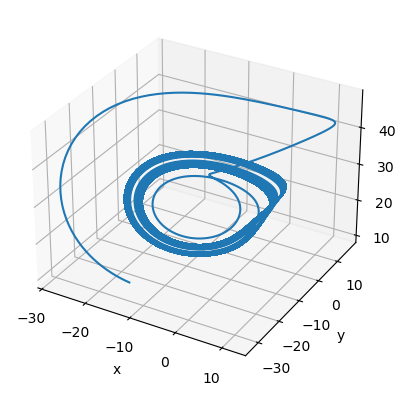
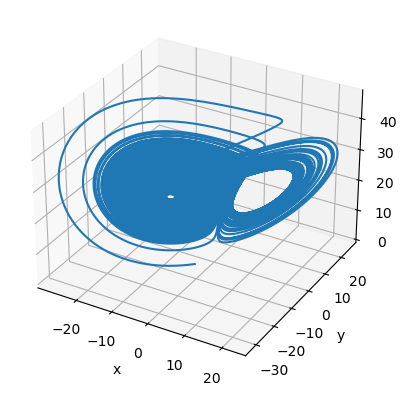
[8]:
runner = bp.IntegratorRunner(
lu_chen_system,
monitors=['x', 'y', 'z'],
inits=dict(x=0.1, y=0.3, z=-0.6),
dt=0.002
)
run_and_visualize(runner, 100, args=dict(u=11),)
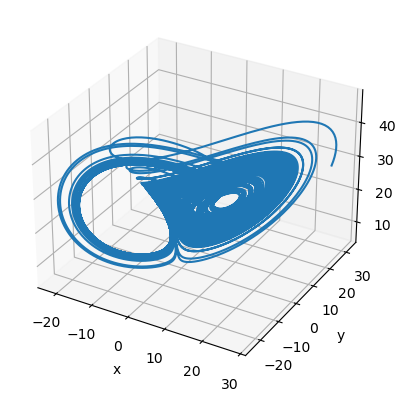
[9]:
runner = bp.IntegratorRunner(
lu_chen_system,
monitors=['x', 'y', 'z'],
inits=dict(x=0.1, y=0.3, z=-0.6),
dt=0.002
)
run_and_visualize(runner, 100, args=dict(u=12),)
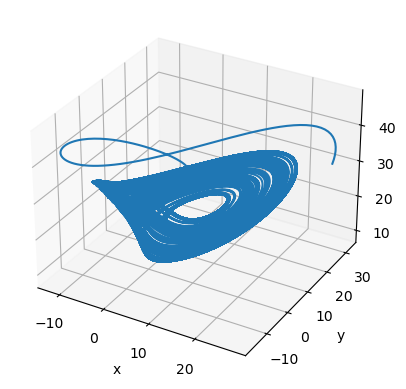
Modified Lu Chen attractor
System equations:
where
[10]:
class ModifiedLuChenSystem(bp.Dynamic):
def __init__(self, num, a=35, b=3, c=28, d0=1, d1=1, d2=0., tau=.2, dt=0.1):
super(ModifiedLuChenSystem, self).__init__(num)
# parameters
self.a = a
self.b = b
self.c = c
self.d0 = d0
self.d1 = d1
self.d2 = d2
self.tau = tau
self.delay_len = int(tau/dt)
# variables
self.z = bm.Variable(bm.ones(num) * 14)
self.z_delay = bm.LengthDelay(self.z,
delay_len=self.delay_len,
initial_delay_data=14.)
self.x = bm.Variable(bm.ones(num))
self.y = bm.Variable(bm.ones(num))
# functions
def derivative(x, y, z, t, z_delay):
dx = self.a * (y - x)
f = self.d0 * z + self.d1 * z_delay - self.d2 * bm.sin(z_delay)
dy = (self.c - self.a) * x - x * f + self.c * y
dz = x * y - self.b * z
return dx, dy, dz
self.integral = bp.odeint(derivative, method='rk4')
def update(self):
self.x.value, self.y.value, self.z.value = self.integral(
self.x.value, self.y.value, self.z.value, bp.share['t'],
self.z_delay(self.delay_len), bp.share['dt']
)
self.z_delay.update(self.z)
[11]:
runner = bp.DSRunner(ModifiedLuChenSystem(1, dt=0.001),
monitors=['x', 'y', 'z'],
dt=0.001)
run_and_visualize(runner, 50)
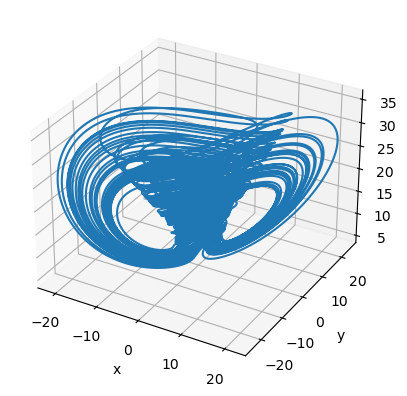
Chua’s system
The classic Chua’s system is described by the following dimensionless equations [3]
where \(\alpha\), \(\beta\), and \(\gamma\) are constant parameters and
with \(a,b\) being the slopes of the inner and outer segments of \(f(x)\). Note that the parameterγis usually ignored; that is, \(\gamma=0\).
[12]:
@bp.odeint(method='rk4')
def chua_system(x, y, z, t, alpha=10, beta=14.514, gamma=0, a=-1.197, b=-0.6464):
fx = b * x + 0.5 * (a - b) * (bm.abs(x + 1) - bm.abs(x - 1))
dx = alpha * (y - x) - alpha * fx
dy = x - y + z
dz = -beta * y - gamma * z
return dx, dy, dz
[13]:
runner = bp.IntegratorRunner(
chua_system,
monitors=['x', 'y', 'z'],
inits=dict(x=0.001, y=0, z=0.),
dt=0.002
)
run_and_visualize(runner, 100)
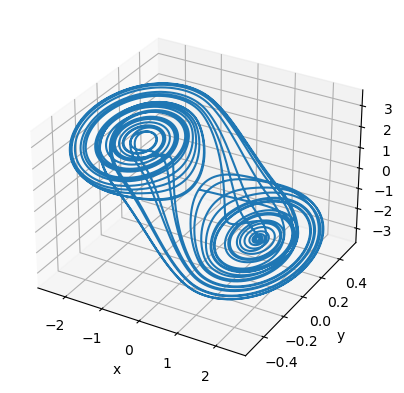
[14]:
runner = bp.IntegratorRunner(
chua_system,
monitors=['x', 'y', 'z'],
inits=dict(x=9.4287, y=-0.5945, z=-13.4705),
dt=0.002
)
run_and_visualize(runner, 100, args=dict(alpha=8.8, beta=12.0732, gamma=0.0052, a=-0.1768, b=-1.1468),)
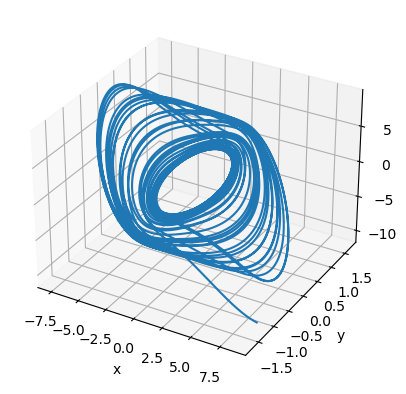
[15]:
runner = bp.IntegratorRunner(
chua_system,
monitors=['x', 'y', 'z'],
inits=dict(x=[-6.0489, 6.0489],
y=[0.0839, -0.0839],
z=[8.7739, -8.7739]),
dt=0.002
)
run_and_visualize(runner, 100, args=dict(alpha=8.4562, beta=12.0732, gamma=0.0052, a=-0.1768, b=-1.1468),)
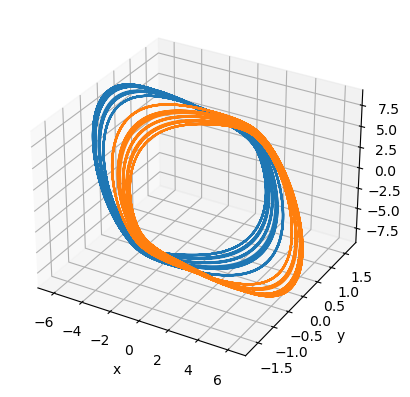
Modified Chua chaotic attractor
In 2001, Tang et al. proposed a modified Chua chaotic system:
where
[16]:
@bp.odeint(method='rk4')
def modified_chua_system(x, y, z, t, alpha=10.82, beta=14.286, a=1.3, b=.11, d=0):
dx = alpha * (y + b * bm.sin(bm.pi * x / 2 / a + d))
dy = x - y + z
dz = -beta * y
return dx, dy, dz
[17]:
runner = bp.IntegratorRunner(
modified_chua_system,
monitors=['x', 'y', 'z'],
inits=dict(x=1, y=1, z=0.),
dt=0.01
)
run_and_visualize(runner, 1000)
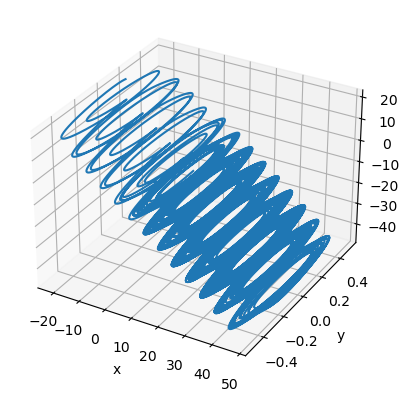
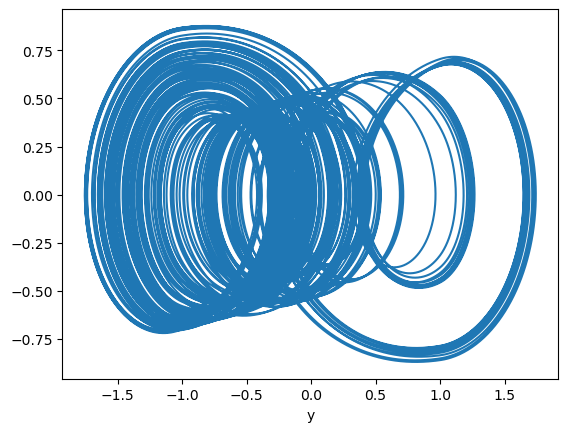
PWL Duffing chaotic attractor
Aziz Alaoui investigated PWL Duffing equation in 2000:
[18]:
@bp.odeint(method='rk4')
def PWL_duffing_eq(x, y, t, e=0.25, m0=-0.0845, m1=0.66, omega=1, i=-14):
gamma = 0.14 + i / 20
dx = y
dy = -m1 * x - (0.5 * (m0 - m1)) * (abs(x + 1) - abs(x - 1)) - e * y + gamma * bm.cos(omega * t)
return dx, dy
[19]:
runner = bp.IntegratorRunner(
PWL_duffing_eq,
monitors=['x', 'y'],
inits=dict(x=0, y=0),
dt=0.01
)
run_and_visualize(runner, 1000, dim=2)
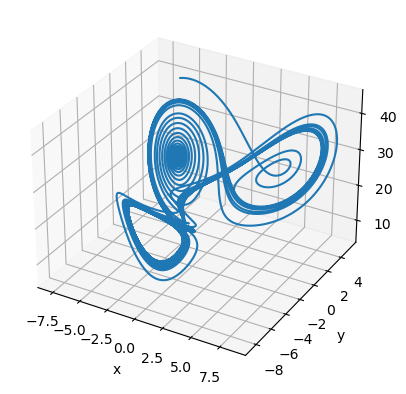
Modified Lorenz chaotic system
Miranda & Stone proposed a modified Lorenz system:
[20]:
@bp.odeint(method='euler')
def modified_Lorenz(x, y, z, t, a=10, b=8 / 3, c=137 / 5):
temp = 3 * bm.sqrt(x * x + y * y)
dx = (-(a + 1) * x + a - c + z * y) / 3 + ((1 - a) * (x * x - y * y) + (2 * (a + c - z)) * x * y) / temp
dy = ((c - a - z) * x - (a + 1) * y) / 3 + (2 * (a - 1) * x * y + (a + c - z) * (x * x - y * y)) / temp
dz = (3 * x * x * y - y * y * y) / 2 - b * z
return dx, dy, dz
[21]:
runner = bp.IntegratorRunner(
modified_Lorenz,
monitors=['x', 'y', 'z'],
inits=dict(x=-8, y=4, z=10),
dt=0.001
)
run_and_visualize(runner, 100, dim=3)
References
[1] CHEN, GUANRONG; UETA, TETSUSHI (July 1999). “Yet Another Chaotic Attractor”. International Journal of Bifurcation and Chaos. 09 (7): 1465–1466.
[2] Chen, Guanrong; Jinhu Lu (2006). “Generating Multiscroll Chaotic Attractors: Theories, Methods and Applications” (PDF). International Journal of Bifurcation and Chaos. 16 (4): 775–858. Bibcode:2006IJBC…16..775L. doi:10.1142/s0218127406015179. Retrieved 2012-02-16.
[3] L. Fortuna, M. Frasca, and M. G. Xibilia, “Chuas circuit implementations: yesterday, today and tomorrow,” World Scientific, 2009.
