Logistic map
The logistic map is a one-dimensional discrete time dynamical system that is defined by the equation
\[x_{n+1} =\lambda x_{n}(1-x_{n})\]
For an initial value \(0\leq x_{0}\leq1\) this map generates a sequence of values \(x_{0},x_{1},...x_{n},x_{n+1},...\) The growth parameter is chosen to be
\[0<\lambda\leq4\]
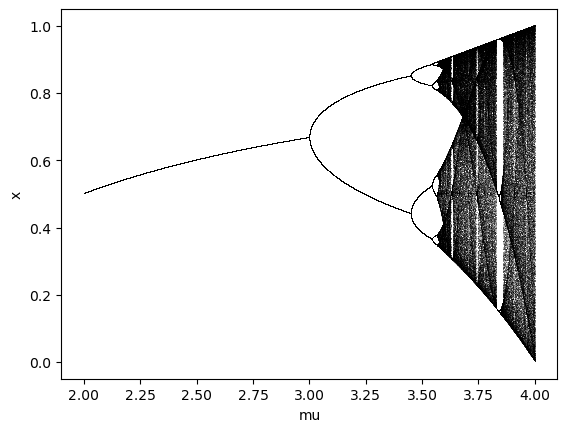
which implies that for all \(n\) the state variable will remain bounded in the unit interval. Despite its simplicity this famous dynamical system can exhibit an unbelievable dynamic richness.
[1]:
import brainpy as bp
import brainpy.math as bm
import matplotlib.pyplot as plt
[2]:
bp.__version__
[2]:
'2.4.3'
[3]:
class LogisticMap(bp.Dynamic):
def __init__(self, num, mu0=2., mu1=4.):
super(LogisticMap, self).__init__(num)
self.mu = bm.linspace(mu0, mu1, num)
self.x = bm.Variable(bm.ones(num) * 0.2)
def update(self):
self.x.value = self.mu * self.x * ( 1- self.x)
[4]:
map = LogisticMap(10000, 2, 4)
No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.)
[5]:
runner = bp.DSRunner(map, monitors=['x'], dt=1.)
runner.run(1100)
[6]:
plt.plot(map.mu, runner.mon.x[1000:].T, ',k', alpha=0.25)
plt.xlabel('mu')
plt.ylabel('x')
plt.show()