[1D] Simple systems

import brainpy as bp

bp.math.enable_x64()
# bp.math.set_platform('cpu')

bp.__version__

'2.4.3'

Phase plane

Here we will show the birfurcation analysis of 1D system with dummy test neuronal model.

\[\dot{x} = x^3-x + I\]

First, let’s define the model.

@bp.odeint
def int_x(x, t, Iext):
  dx = x ** 3 - x + Iext
  return dx

analyzer = bp.analysis.PhasePlane1D(int_x,
                                    target_vars={'x': [-10, 10]},
                                    pars_update={'Iext': 0.})
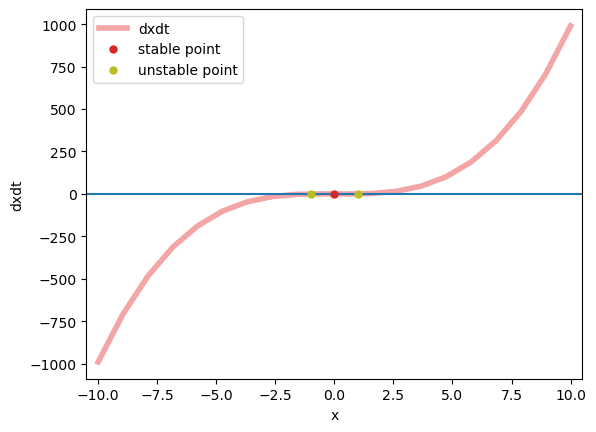
analyzer.plot_vector_field()
analyzer.plot_fixed_point(show=True)

No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.)
I am creating the vector field ...
I am searching fixed points ...
Fixed point #1 at x=-1.0000000000000002 is a unstable point.
Fixed point #2 at x=-7.771561172376096e-16 is a stable point.
Fixed point #3 at x=1.0000000000000002 is a unstable point.

Codimension1

Then, create a bifurcation analyzer with bp.symbolic.Bifurcation.

an = bp.analysis.Bifurcation1D(
  int_x,
  target_pars={'Iext': [-0.5, 0.5]},
  target_vars={"x": [-2, 2]},
  resolutions={'Iext': 0.001}
)
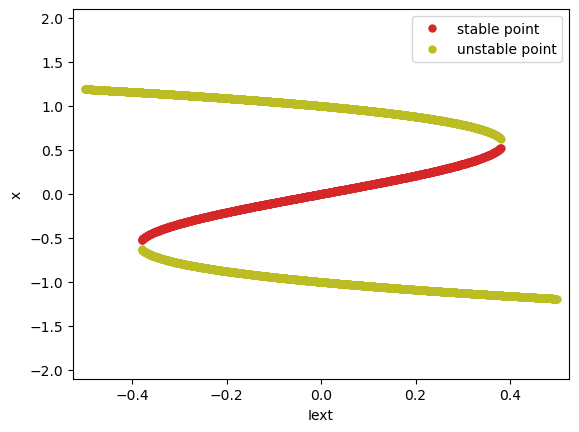
an.plot_bifurcation(show=True)

I am making bifurcation analysis ...

Codimension2

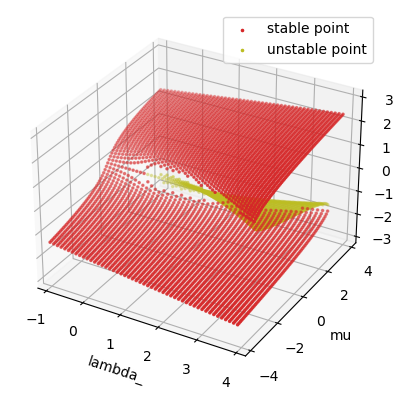
Here we define the following 1D model for codimension 2 bifurcation testing.

\[\dot{x} = \mu+ \lambda x - x^3\]

@bp.odeint
def int_x(x, t, mu, lambda_):
  dxdt = mu + lambda_ * x - x ** 3
  return dxdt

analyzer = bp.analysis.Bifurcation1D(
  int_x,
  target_pars={'lambda_': [-1, 4], 'mu': [-4, 4], },
  target_vars={'x': [-3, 3]},
  resolutions={'lambda_': 0.1, 'mu': 0.1}
)
analyzer.plot_bifurcation(show=True)

I am making bifurcation analysis ...