Gap junction-coupled FitzHugh-Nagumo Model
[1]:
import brainpy as bp
import brainpy.math as bm
# bp.math.set_platform('cpu')
bp.math.enable_x64()
bp.__version__
[1]:
'2.4.3'
[2]:
class GJCoupledFHN(bp.DynamicalSystem):
def __init__(self, num=2, method='exp_auto'):
super(GJCoupledFHN, self).__init__()
# parameters
self.num = num
self.a = 0.7
self.b = 0.8
self.tau = 12.5
self.gjw = 0.0001
# variables
self.V = bm.Variable(bm.random.uniform(-2, 2, num))
self.w = bm.Variable(bm.random.uniform(-2, 2, num))
self.Iext = bm.Variable(bm.zeros(num))
# functions
self.int_V = bp.odeint(self.dV, method=method)
self.int_w = bp.odeint(self.dw, method=method)
def dV(self, V, t, w, Iext=0.):
gj = (V.reshape((-1, 1)) - V).sum(axis=0) * self.gjw
dV = V - V * V * V / 3 - w + Iext + gj
return dV
def dw(self, w, t, V):
dw = (V + self.a - self.b * w) / self.tau
return dw
def update(self):
tdi = bp.share.get_shargs()
self.V.value = self.int_V(self.V, tdi.t, self.w, self.Iext, tdi.dt)
self.w.value = self.int_w(self.w, tdi.t, self.V, tdi.dt)
[3]:
def analyze_net(num=2, gjw=0.01, Iext=bm.asarray([0., 0.6])):
assert isinstance(Iext, (int, float)) or (len(Iext) == num)
model = GJCoupledFHN(num)
model.gjw = gjw
model.Iext[:] = Iext
# simulation
runner = bp.DSRunner(model, monitors=['V'])
runner.run(300.)
bp.visualize.line_plot(runner.mon.ts, runner.mon.V, legend='V',
plot_ids=list(range(model.num)), show=True)
# analysis
finder = bp.analysis.SlowPointFinder(f_cell=model,
target_vars={'V': model.V, 'w': model.w})
finder.find_fps_with_gd_method(
candidates={'V': bm.random.normal(0., 2., (1000, model.num)),
'w': bm.random.normal(0., 2., (1000, model.num))},
tolerance=1e-5,
num_batch=200,
optimizer=bp.optim.Adam(lr=bp.optim.ExponentialDecay(0.05, 1, 0.9999)),
)
finder.filter_loss(1e-8)
finder.keep_unique()
print('fixed_points: ', finder.fixed_points)
print('losses:', finder.losses)
_ = finder.compute_jacobians(finder.fixed_points, plot=True)
No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.)
4D system
[4]:
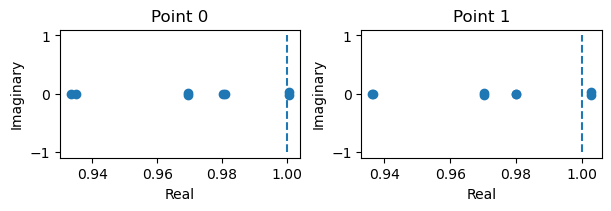
analyze_net(num=2, gjw=0.1, Iext=bm.asarray([0., 0.6]))
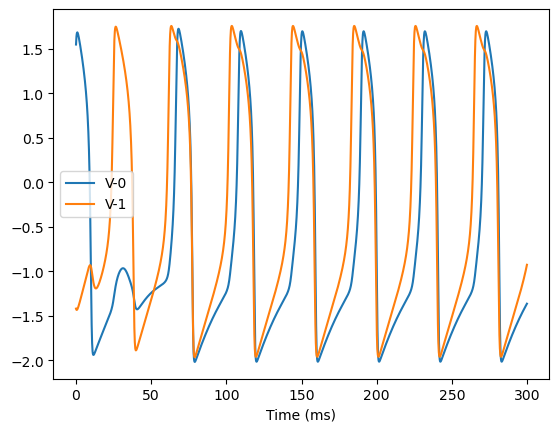
Optimizing with Adam(lr=ExponentialDecay(0.05, decay_steps=1, decay_rate=0.9999), last_call=-1), beta1=0.9, beta2=0.999, eps=1e-08) to find fixed points:
Batches 1-200 in 0.81 sec, Training loss 0.0002788616
Batches 201-400 in 0.48 sec, Training loss 0.0002076722
Batches 401-600 in 0.58 sec, Training loss 0.0001604245
Batches 601-800 in 0.52 sec, Training loss 0.0001257214
Batches 801-1000 in 0.55 sec, Training loss 0.0000993401
Batches 1001-1200 in 0.25 sec, Training loss 0.0000791463
Batches 1201-1400 in 0.64 sec, Training loss 0.0000634978
Batches 1401-1600 in 0.35 sec, Training loss 0.0000512977
Batches 1601-1800 in 0.57 sec, Training loss 0.0000417576
Batches 1801-2000 in 0.41 sec, Training loss 0.0000342319
Batches 2001-2200 in 0.50 sec, Training loss 0.0000282288
Batches 2201-2400 in 0.59 sec, Training loss 0.0000234155
Batches 2401-2600 in 0.50 sec, Training loss 0.0000195315
Batches 2601-2800 in 0.58 sec, Training loss 0.0000164139
Batches 2801-3000 in 0.40 sec, Training loss 0.0000138706
Batches 3001-3200 in 0.59 sec, Training loss 0.0000118313
Batches 3201-3400 in 0.33 sec, Training loss 0.0000101996
Batches 3401-3600 in 0.72 sec, Training loss 0.0000088474
Stop optimization as mean training loss 0.0000088474 is below tolerance 0.0000100000.
Excluding fixed points with squared speed above tolerance 1e-08:
Kept 372/1000 fixed points with tolerance under 1e-08.
Excluding non-unique fixed points:
Kept 1/372 unique fixed points with uniqueness tolerance 0.025.
fixed_points: {'V': array([[-1.17315378, -0.73803683]]), 'w': array([[-0.59144223, -0.04754604]])}
losses: [1.781621e-27]
C:\Users\adadu\miniconda3\envs\brainpy\lib\site-packages\jax\_src\numpy\array_methods.py:329: FutureWarning: The arr.split() method is deprecated. Use jax.numpy.split instead.
warnings.warn(
[5]:
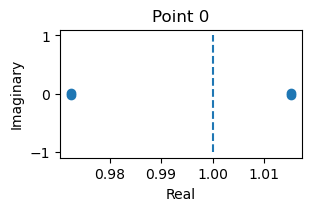
analyze_net(num=2, gjw=0.1, Iext=bm.asarray([0., 0.1]))
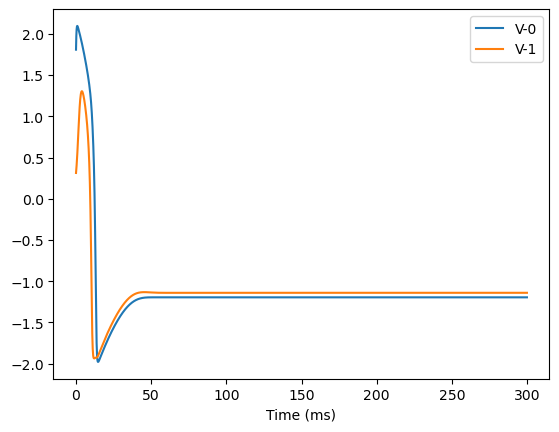
Optimizing with Adam(lr=ExponentialDecay(0.05, decay_steps=1, decay_rate=0.9999), last_call=-1), beta1=0.9, beta2=0.999, eps=1e-08) to find fixed points:
Batches 1-200 in 0.42 sec, Training loss 0.0002744392
Batches 201-400 in 0.63 sec, Training loss 0.0002038559
Batches 401-600 in 0.27 sec, Training loss 0.0001579408
Batches 601-800 in 0.71 sec, Training loss 0.0001249296
Batches 801-1000 in 0.34 sec, Training loss 0.0001004665
Batches 1001-1200 in 0.60 sec, Training loss 0.0000817813
Batches 1201-1400 in 0.45 sec, Training loss 0.0000672077
Batches 1401-1600 in 0.48 sec, Training loss 0.0000557249
Batches 1601-1800 in 0.48 sec, Training loss 0.0000465356
Batches 1801-2000 in 0.45 sec, Training loss 0.0000391051
Batches 2001-2200 in 0.58 sec, Training loss 0.0000330272
Batches 2201-2400 in 0.46 sec, Training loss 0.0000280838
Batches 2401-2600 in 0.61 sec, Training loss 0.0000240266
Batches 2601-2800 in 0.36 sec, Training loss 0.0000206586
Batches 2801-3000 in 0.64 sec, Training loss 0.0000178943
Batches 3001-3200 in 0.28 sec, Training loss 0.0000155499
Batches 3201-3400 in 0.65 sec, Training loss 0.0000135563
Batches 3401-3600 in 0.29 sec, Training loss 0.0000119020
Batches 3601-3800 in 0.63 sec, Training loss 0.0000105507
Batches 3801-4000 in 0.39 sec, Training loss 0.0000094129
Stop optimization as mean training loss 0.0000094129 is below tolerance 0.0000100000.
Excluding fixed points with squared speed above tolerance 1e-08:
Kept 535/1000 fixed points with tolerance under 1e-08.
Excluding non-unique fixed points:
Kept 1/535 unique fixed points with uniqueness tolerance 0.025.
fixed_points: {'V': array([[-1.19613886, -1.14106509]]), 'w': array([[-0.62017365, -0.55133897]])}
losses: [1.17769156e-15]
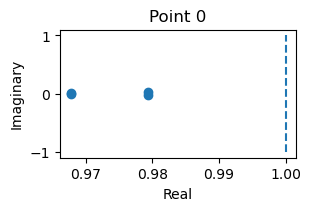
8D system
[6]:
analyze_net(num=4, gjw=0.1, Iext=bm.asarray([0., 0., 0., 0.6]))
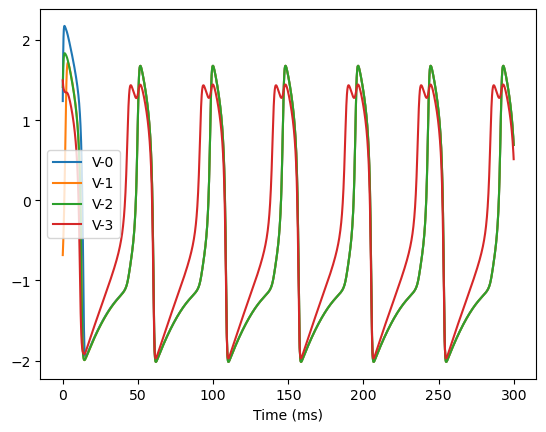
Optimizing with Adam(lr=ExponentialDecay(0.05, decay_steps=1, decay_rate=0.9999), last_call=-1), beta1=0.9, beta2=0.999, eps=1e-08) to find fixed points:
Batches 1-200 in 0.41 sec, Training loss 0.0002981253
Batches 201-400 in 0.20 sec, Training loss 0.0002175304
Batches 401-600 in 0.21 sec, Training loss 0.0001681047
Batches 601-800 in 0.22 sec, Training loss 0.0001327457
Batches 801-1000 in 0.24 sec, Training loss 0.0001062666
Batches 1001-1200 in 0.20 sec, Training loss 0.0000860732
Batches 1201-1400 in 0.20 sec, Training loss 0.0000704338
Batches 1401-1600 in 0.21 sec, Training loss 0.0000581533
Batches 1601-1800 in 0.22 sec, Training loss 0.0000483691
Batches 1801-2000 in 0.22 sec, Training loss 0.0000405031
Batches 2001-2200 in 0.22 sec, Training loss 0.0000341309
Batches 2201-2400 in 0.22 sec, Training loss 0.0000289916
Batches 2401-2600 in 0.22 sec, Training loss 0.0000248071
Batches 2601-2800 in 0.22 sec, Training loss 0.0000213434
Batches 2801-3000 in 0.22 sec, Training loss 0.0000184814
Batches 3001-3200 in 0.23 sec, Training loss 0.0000161170
Batches 3201-3400 in 0.29 sec, Training loss 0.0000141462
Batches 3401-3600 in 0.20 sec, Training loss 0.0000125133
Batches 3601-3800 in 0.20 sec, Training loss 0.0000111212
Batches 3801-4000 in 0.20 sec, Training loss 0.0000099064
Stop optimization as mean training loss 0.0000099064 is below tolerance 0.0000100000.
Excluding fixed points with squared speed above tolerance 1e-08:
Kept 313/1000 fixed points with tolerance under 1e-08.
Excluding non-unique fixed points:
Kept 2/313 unique fixed points with uniqueness tolerance 0.025.
fixed_points: {'V': array([[-1.17876245, -1.17875408, -1.1875546 , -0.81695988],
[-1.17414082, -1.17455959, -1.17427155, -0.79030303]]), 'w': array([[-0.5975094 , -0.59751575, -0.59054519, -0.14463357],
[-0.59622882, -0.59590929, -0.59613388, -0.14083089]])}
losses: [3.68611836e-09 8.30820343e-09]