(Teka, et. al, 2018): Fractional-order Izhikevich neuron model

Implementation of the model:

Teka, Wondimu W., Ranjit Kumar Upadhyay, and Argha Mondal. “Spiking and bursting patterns of fractional-order Izhikevich model.” Communications in Nonlinear Science and Numerical Simulation 56 (2018): 161-176.

[1]:

import brainpy as bp

import matplotlib.pyplot as plt

[2]:

def run_model(dt=0.1, duration=500, alpha=1.0):
    inputs, length = bp.inputs.section_input([0, 10], [50, duration],
                                              dt=dt, return_length=True)
    neuron = bp.neurons.FractionalIzhikevich(1, num_memory=int(length / dt), alpha=alpha)
    runner = bp.DSRunner(neuron,
                         monitors=['V'],
                         inputs=['input', inputs, 'iter'],
                         dt=dt)
    runner.run(length)

    plt.plot(runner.mon.ts, runner.mon.V.flatten())
    plt.xlabel('Time [ms]')
    plt.ylabel('Potential [mV]')
    plt.title(r'$\alpha$=' + str(alpha))
    plt.show()

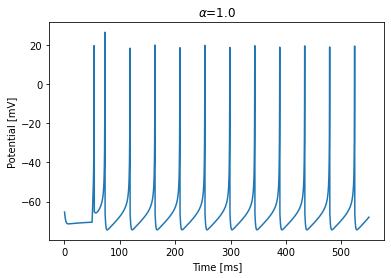
Regular spiking

[3]:

run_model(dt=0.1, duration=500, alpha=1.0)

WARNING:jax._src.lib.xla_bridge:No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.)

../_images/neurons_2018_Fractional_Izhikevich_model_5_2.png

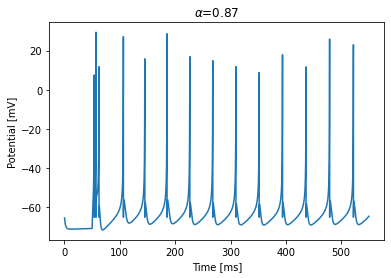
Intrinsically bursting

[4]:

run_model(dt=0.1, duration=500, alpha=0.87)

../_images/neurons_2018_Fractional_Izhikevich_model_7_1.png

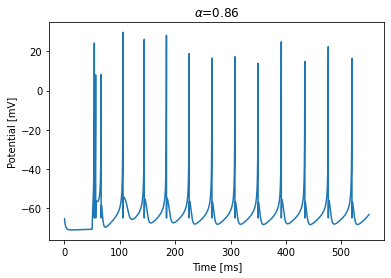
Mixed Mode (Irregular)

[5]:

run_model(dt=0.1, duration=500, alpha=0.86)

../_images/neurons_2018_Fractional_Izhikevich_model_9_1.png

Chattering

[6]:

run_model(dt=0.1, duration=500, alpha=0.8)

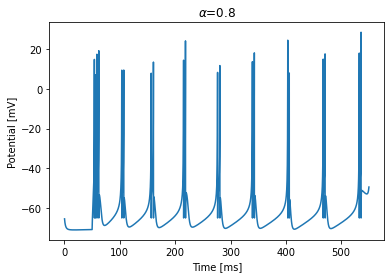
../_images/neurons_2018_Fractional_Izhikevich_model_11_1.png

Bursting

[7]:

run_model(dt=0.1, duration=1000, alpha=0.7)

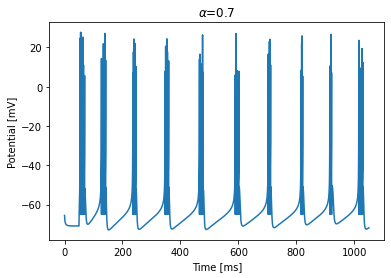
../_images/neurons_2018_Fractional_Izhikevich_model_13_1.png

Bursting with longer bursts

[8]:

run_model(dt=0.1, duration=1000, alpha=0.5)

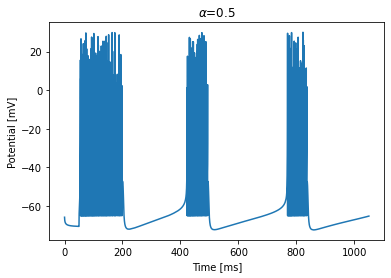
../_images/neurons_2018_Fractional_Izhikevich_model_15_1.png

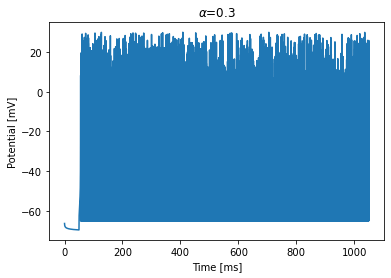
Fast spiking

[9]:

run_model(dt=0.1, duration=1000, alpha=0.3)

../_images/neurons_2018_Fractional_Izhikevich_model_17_1.png