(Mondal, et. al, 2019): Fractional-order FitzHugh-Rinzel bursting neuron model
Implementation of the paper:
Mondal, A., Sharma, S.K., Upadhyay, R.K. et al. Firing activities of a fractional-order FitzHugh-Rinzel bursting neuron model and its coupled dynamics. Sci Rep 9, 15721 (2019). https://doi.org/10.1038/s41598-019-52061-4
[1]:
import brainpy as bp
import matplotlib.pyplot as plt
[2]:
def run_model(model, inputs, length):
runner = bp.DSRunner(model, monitors=['V'], inputs=inputs)
runner.run(length)
return runner
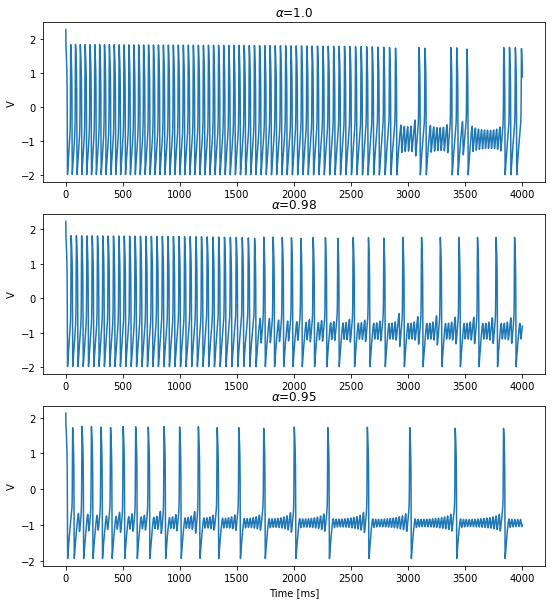
Parameter set 1
[3]:
dt = 0.1
Iext = 0.3125
duration = 4000
neuron_pars = dict(a=0.7, b=0.8, c=-0.775, d=1., delta=0.08, mu=0.0001,
w_initializer=bp.init.Constant(-0.1),
y_initializer=bp.init.Constant(0.1))
[4]:
alphas = [1.0, 0.98, 0.95]
plt.figure(figsize=(9, 10))
for i, alpha in enumerate(alphas):
neuron = bp.neurons.FractionalFHR(1,
alpha=alpha,
num_memory=4000,
**neuron_pars)
runner = run_model(neuron, inputs=['input', Iext], length=duration)
plt.subplot(len(alphas), 1, i+1)
plt.plot(runner.mon.ts, runner.mon.V[:, 0])
plt.title(r'$\alpha$=' + str(alphas[i]))
plt.ylabel('V')
plt.xlabel('Time [ms]')
plt.show()
WARNING:jax._src.lib.xla_bridge:No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.)
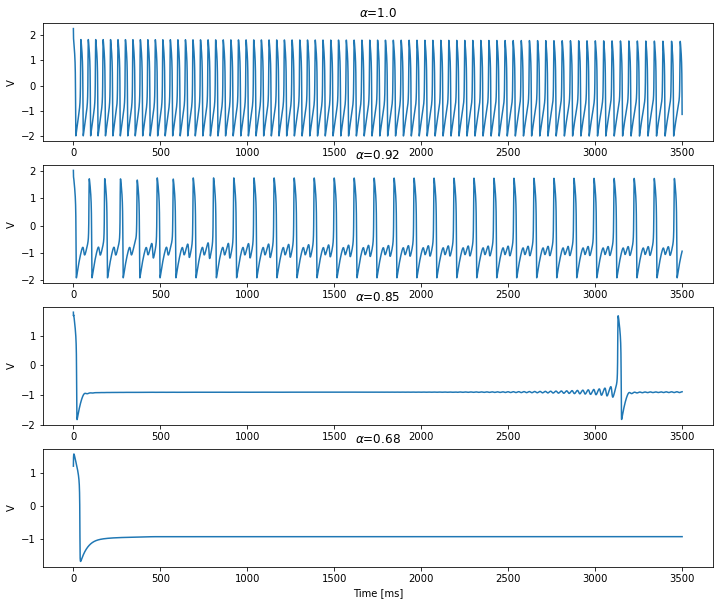
Parameter set 2
[5]:
Iext = 0.4
duration = 3500
neuron_pars = dict(a=0.7, b=0.8, c=-0.775, d=1., delta=0.08, mu=0.0001)
[6]:
alphas = [1.0, 0.92, 0.85, 0.68]
plt.figure(figsize=(12, 10))
for i, alpha in enumerate(alphas):
neuron = bp.neurons.FractionalFHR(1,
alpha=alpha,
num_memory=4000,
**neuron_pars)
runner = run_model(neuron, inputs=['input', Iext], length=duration)
plt.subplot(len(alphas), 1, i+1)
plt.plot(runner.mon.ts, runner.mon.V[:, 0])
plt.title(r'$\alpha$=' + str(alphas[i]))
plt.ylabel('V')
plt.xlabel('Time [ms]')
plt.show()
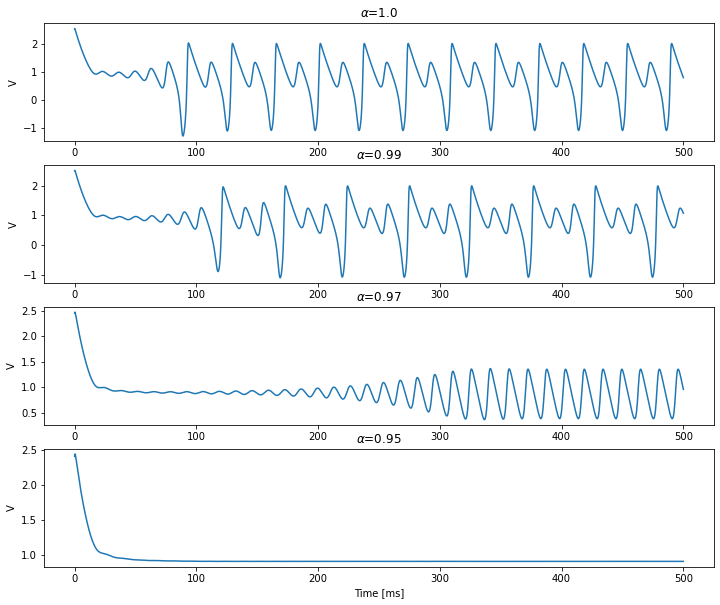
Parameter set 3
[7]:
Iext = 3
duration = 500
neuron_pars = dict(a=0.7, b=0.8, c=-0.775, d=1., delta=0.08, mu=0.18)
[8]:
alphas = [1.0, 0.99, 0.97, 0.95]
plt.figure(figsize=(12, 10))
for i, alpha in enumerate(alphas):
neuron = bp.neurons.FractionalFHR(1,
alpha=alpha,
**neuron_pars)
runner = run_model(neuron, inputs=['input', Iext], length=duration)
plt.subplot(len(alphas), 1, i+1)
plt.plot(runner.mon.ts, runner.mon.V[:, 0])
plt.title(r'$\alpha$=' + str(alphas[i]))
plt.ylabel('V')
plt.xlabel('Time [ms]')
plt.show()
Parameter set 4
[9]:
Iext = 0.3125
duration = 3500
neuron_pars = dict(a=0.7, b=0.8, c=1.3, d=1., delta=0.08, mu=0.0001)
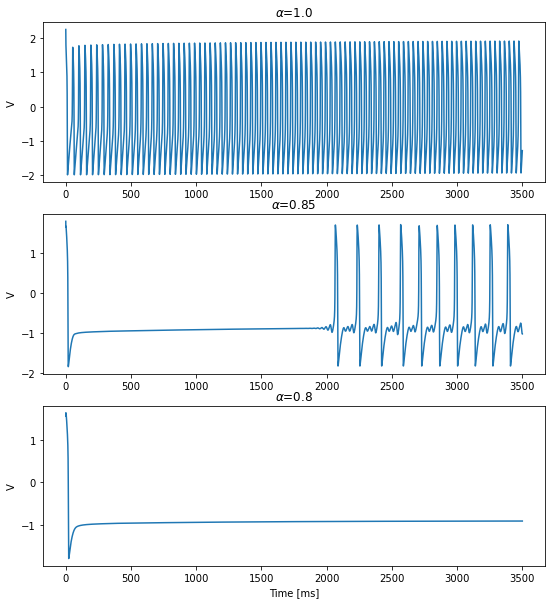
[10]:
alphas = [1.0, 0.85, 0.80]
plt.figure(figsize=(9, 10))
for i, alpha in enumerate(alphas):
neuron = bp.neurons.FractionalFHR(1,
alpha=alpha,
num_memory=3000,
**neuron_pars)
runner = run_model(neuron, inputs=['input', Iext], length=duration)
plt.subplot(len(alphas), 1, i+1)
plt.plot(runner.mon.ts, runner.mon.V[:, 0])
plt.title(r'$\alpha$=' + str(alphas[i]))
plt.ylabel('V')
plt.xlabel('Time [ms]')
plt.show()
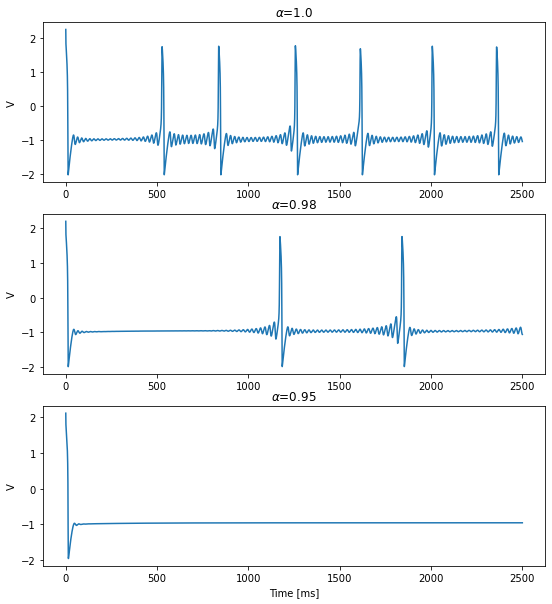
Parameter set 5
[11]:
Iext = 0.3125
duration = 2500
neuron_pars = dict(a=0.7, b=0.8, c=-0.908, d=1., delta=0.08, mu=0.002)
[12]:
alphas = [1.0, 0.98, 0.95]
plt.figure(figsize=(9, 10))
for i, alpha in enumerate(alphas):
neuron = bp.neurons.FractionalFHR(1, alpha=alpha, **neuron_pars)
runner = run_model(neuron, inputs=['input', Iext], length=duration)
plt.subplot(len(alphas), 1, i+1)
plt.plot(runner.mon.ts, runner.mon.V[:, 0])
plt.title(r'$\alpha$=' + str(alphas[i]))
plt.ylabel('V')
plt.xlabel('Time [ms]')
plt.show()