(Bellec, et. al, 2020): eprop for Evidence Accumulation Task

Implementation of the paper:

• Bellec, G., Scherr, F., Subramoney, A., Hajek, E., Salaj, D., Legenstein, R., & Maass, W. (2020). A solution to the learning dilemma for recurrent networks of spiking neurons. Nature communications, 11(1), 1-15.

import brainpy as bp
import brainpy.math as bm
import matplotlib.pyplot as plt
import numpy as np
from jax.lax import stop_gradient
from matplotlib import patches

bm.set_environment(bm.training_mode, dt=1.)

bp.__version__

'2.4.3'

# training parameters
n_batch = 128  # batch size

# neuron model and simulation parameters
reg_f = 1.  # regularization coefficient for firing rate
reg_rate = 10  # target firing rate for regularization [Hz]

# Experiment parameters
t_cue_spacing = 150  # distance between two consecutive cues in ms

# Frequencies
input_f0 = 40. / 1000.  # poisson firing rate of input neurons in khz
regularization_f0 = reg_rate / 1000.  # mean target network firing frequency

class EligSNN(bp.DynSysGroup):
  def __init__(self, num_in, num_rec, num_out, eprop=True, tau_a=2e3, tau_v=2e1):
    super(EligSNN, self).__init__()

    # parameters
    self.num_in = num_in
    self.num_rec = num_rec
    self.num_out = num_out
    self.eprop = eprop

    # neurons
    self.o = bp.dyn.Leaky(num_out, tau=20)

    n_regular = int(num_rec / 2)
    n_adaptive = num_rec - n_regular
    beta1 = bm.exp(- bm.get_dt() / tau_a)
    beta2 = 1.7 * (1 - beta1) / (1 - bm.exp(-1 / tau_v))
    beta = bm.concatenate([bm.ones(n_regular), bm.ones(n_adaptive) * beta2])
    self.r = bp.neurons.ALIFBellec2020(
      num_rec,
      V_rest=0.,
      tau_ref=5.,
      V_th=0.6,
      tau_a=tau_a,
      tau=tau_v,
      beta=beta,
      V_initializer=bp.init.ZeroInit(),
      a_initializer=bp.init.ZeroInit(),
      eprop=eprop,
      input_var=False,
    )

    # synapses
    self.i2r = bp.layers.Dense(num_in, num_rec,
                               W_initializer=bp.init.KaimingNormal(),
                               b_initializer=None)
    self.i2r.W *= tau_v
    self.r2r = bp.layers.Dense(num_rec, num_rec,
                               W_initializer=bp.init.KaimingNormal(),
                               b_initializer=None)
    self.r2r.W *= tau_v
    self.r2o = bp.layers.Dense(num_rec, num_out,
                               W_initializer=bp.init.KaimingNormal(),
                               b_initializer=None)

  def update(self, x):
    z = stop_gradient(self.r.spike.value) if self.eprop else self.r.spike.value
    return self.o(self.r2o(self.r(self.r2r(z) + self.i2r(x))))

net = EligSNN(num_in=40, num_rec=100, num_out=2, eprop=False)

No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.)

@bp.tools.numba_jit
def generate_click_task_data(batch_size, seq_len, n_neuron, recall_duration, prob, f0=0.5,
                             n_cues=7, t_cue=100, t_interval=150, n_input_symbols=4):
  n_channel = n_neuron // n_input_symbols

  # assign input spike probabilities
  probs = np.where(np.random.random((batch_size, 1)) < 0.5, prob, 1 - prob)

  # for each example in batch, draw which cues are going to be active (left or right)
  cue_assignments = np.asarray(np.random.random(n_cues) > probs, dtype=np.int_)

  # generate input nums - 0: left, 1: right, 2:recall, 3:background noise
  input_nums = 3 * np.ones((batch_size, seq_len), dtype=np.int_)
  input_nums[:, :n_cues] = cue_assignments
  input_nums[:, -1] = 2

  # generate input spikes
  input_spike_prob = np.zeros((batch_size, seq_len, n_neuron))
  d_silence = t_interval - t_cue
  for b in range(batch_size):
    for k in range(n_cues):
      # input channels only fire when they are selected (left or right)
      c = cue_assignments[b, k]
      # reverse order of cues
      i_seq = d_silence + k * t_interval
      i_neu = c * n_channel
      input_spike_prob[b, i_seq:i_seq + t_cue, i_neu:i_neu + n_channel] = f0
  # recall cue
  input_spike_prob[:, -recall_duration:, 2 * n_channel:3 * n_channel] = f0
  # background noise
  input_spike_prob[:, :, 3 * n_channel:] = f0 / 4.
  input_spikes = input_spike_prob > np.random.rand(*input_spike_prob.shape)

  # generate targets
  target_mask = np.zeros((batch_size, seq_len), dtype=np.bool_)
  target_mask[:, -1] = True
  target_nums = (np.sum(cue_assignments, axis=1) > n_cues / 2).astype(np.int_)
  return input_spikes, input_nums, target_nums, target_mask

def get_data(batch_size, n_in, t_interval, f0):
  # used for obtaining a new randomly generated batch of examples
  def generate_data():
    seq_len = int(t_interval * 7 + 1200)
    for _ in range(10):
      spk_data, _, target_data, _ = generate_click_task_data(
        batch_size=batch_size, seq_len=seq_len, n_neuron=n_in, recall_duration=150,
        prob=0.3, t_cue=100, n_cues=7, t_interval=t_interval, f0=f0, n_input_symbols=4
      )
      yield spk_data, target_data

  return generate_data

def loss_fun(predicts, targets):
  predicts, mon = predicts

  # we only use network output at the end for classification
  output_logits = predicts[:, -t_cue_spacing:]

  # Define the accuracy
  y_predict = bm.argmax(bm.mean(output_logits, axis=1), axis=1)
  accuracy = bm.equal(targets, y_predict).astype(bm.dftype()).mean()

  # loss function
  tiled_targets = bm.tile(bm.expand_dims(targets, 1), (1, t_cue_spacing))
  loss_cls = bm.mean(bp.losses.cross_entropy_loss(output_logits, tiled_targets))

  # Firing rate regularization:
  # For historical reason we often use this regularization,
  # but the other one is easier to implement in an "online" fashion by a single agent.
  av = bm.mean(mon['r.spike'], axis=(0, 1)) / bm.get_dt()
  loss_reg_f = bm.sum(bm.square(av - regularization_f0) * reg_f)

  # Aggregate the losses #
  loss = loss_reg_f + loss_cls
  loss_res = {'loss': loss, 'loss reg': loss_reg_f, 'accuracy': accuracy}
  return bm.as_jax(loss), loss_res

Training

# Training
trainer = bp.BPTT(
  net,
  loss_fun,
  loss_has_aux=True,
  optimizer=bp.optim.Adam(lr=0.01),
  monitors={'r.spike': net.r.spike},
)
trainer.fit(get_data(n_batch, n_in=net.num_in, t_interval=t_cue_spacing, f0=input_f0),
            num_epoch=40,
            num_report=10)

Train 10 steps, use 22.2320 s, loss 0.7377254962921143, accuracy 0.5390625, loss reg 0.005111623089760542
Train 20 steps, use 15.0638 s, loss 0.716545045375824, accuracy 0.514843761920929, loss reg 0.0051171244122087955
Train 30 steps, use 14.0460 s, loss 0.667855978012085, accuracy 0.6421875357627869, loss reg 0.005078589078038931
Train 40 steps, use 14.2259 s, loss 0.6604841947555542, accuracy 0.6390625238418579, loss reg 0.005082492250949144
Train 50 steps, use 14.7884 s, loss 0.6183825731277466, accuracy 0.75390625, loss reg 0.005063419230282307
Train 60 steps, use 13.5900 s, loss 0.6300409436225891, accuracy 0.73828125, loss reg 0.005013309884816408
Train 70 steps, use 12.3302 s, loss 0.6099017262458801, accuracy 0.7632812857627869, loss reg 0.005029828753322363
Train 80 steps, use 12.4312 s, loss 0.6055963635444641, accuracy 0.7710937857627869, loss reg 0.005091968458145857
Train 90 steps, use 12.9826 s, loss 0.5236468315124512, accuracy 0.87890625, loss reg 0.00514215137809515
Train 100 steps, use 14.0740 s, loss 0.6193331480026245, accuracy 0.7015625238418579, loss reg 0.005061053670942783
Train 110 steps, use 13.8711 s, loss 0.5161479115486145, accuracy 0.83203125, loss reg 0.00531007070094347
Train 120 steps, use 15.1089 s, loss 0.5361291766166687, accuracy 0.82421875, loss reg 0.005363900680094957
Train 130 steps, use 14.3695 s, loss 0.5290614366531372, accuracy 0.807812511920929, loss reg 0.005314335227012634
Train 140 steps, use 14.2483 s, loss 0.5287856459617615, accuracy 0.807812511920929, loss reg 0.005327278282493353
Train 150 steps, use 14.7074 s, loss 0.5100817084312439, accuracy 0.8226562738418579, loss reg 0.0052220746874809265
Train 160 steps, use 13.9733 s, loss 0.5312628746032715, accuracy 0.797656238079071, loss reg 0.005586487241089344
Train 170 steps, use 13.8966 s, loss 0.5020141005516052, accuracy 0.840624988079071, loss reg 0.005601419601589441
Train 180 steps, use 14.1526 s, loss 0.43055611848831177, accuracy 0.893750011920929, loss reg 0.0053567769937217236
Train 190 steps, use 13.8482 s, loss 0.45254191756248474, accuracy 0.8453125357627869, loss reg 0.00548872584477067
Train 200 steps, use 13.9841 s, loss 0.38400256633758545, accuracy 0.890625, loss reg 0.005844198167324066
Train 210 steps, use 13.3046 s, loss 0.5753456354141235, accuracy 0.7710937857627869, loss reg 0.005971371661871672
Train 220 steps, use 14.2367 s, loss 0.3912326395511627, accuracy 0.897656261920929, loss reg 0.006035380531102419
Train 230 steps, use 14.4323 s, loss 0.41148754954338074, accuracy 0.8734375238418579, loss reg 0.005906714126467705
Train 240 steps, use 14.1844 s, loss 0.4987003803253174, accuracy 0.8101562857627869, loss reg 0.0061345770955085754
Train 250 steps, use 12.5646 s, loss 0.48642775416374207, accuracy 0.8414062857627869, loss reg 0.006346860434859991
Train 260 steps, use 14.6393 s, loss 0.32508450746536255, accuracy 0.9164062738418579, loss reg 0.006236965302377939
Train 270 steps, use 13.2020 s, loss 0.36240264773368835, accuracy 0.910937488079071, loss reg 0.006449358072131872
Train 280 steps, use 12.8719 s, loss 0.3478802442550659, accuracy 0.897656261920929, loss reg 0.006728149950504303
Train 290 steps, use 13.4008 s, loss 0.4019208550453186, accuracy 0.9007812738418579, loss reg 0.006419234909117222
Train 300 steps, use 13.0466 s, loss 0.35507872700691223, accuracy 0.89453125, loss reg 0.006826585624366999
Train 310 steps, use 15.1922 s, loss 0.4435243606567383, accuracy 0.8343750238418579, loss reg 0.006594446487724781
Train 320 steps, use 15.1209 s, loss 0.35496360063552856, accuracy 0.918749988079071, loss reg 0.006413914263248444
Train 330 steps, use 14.4502 s, loss 0.49729785323143005, accuracy 0.83984375, loss reg 0.006805828306823969
Train 340 steps, use 12.5568 s, loss 0.42021608352661133, accuracy 0.858593761920929, loss reg 0.0065525430254638195
Train 350 steps, use 12.9650 s, loss 0.37738633155822754, accuracy 0.8929687738418579, loss reg 0.006996490061283112
Train 360 steps, use 13.0145 s, loss 0.5639444589614868, accuracy 0.784375011920929, loss reg 0.006487939041107893
Train 370 steps, use 12.7010 s, loss 0.4074647128582001, accuracy 0.8890625238418579, loss reg 0.00713128549978137
Train 380 steps, use 12.9542 s, loss 0.45685774087905884, accuracy 0.836718738079071, loss reg 0.007074068766087294
Train 390 steps, use 12.9980 s, loss 0.41870346665382385, accuracy 0.8765625357627869, loss reg 0.006821037270128727
Train 400 steps, use 12.7749 s, loss 0.39798665046691895, accuracy 0.878125011920929, loss reg 0.007030840963125229

Visualization

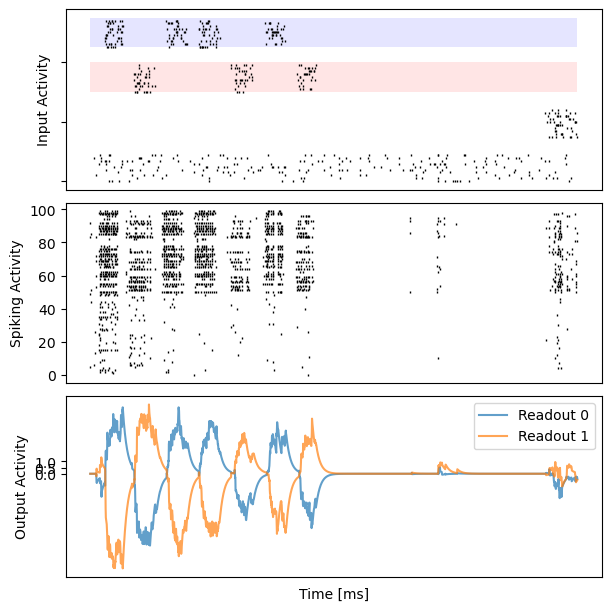
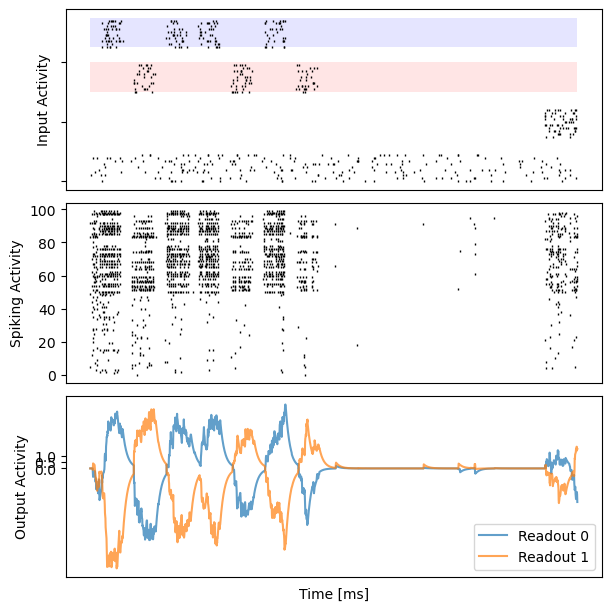
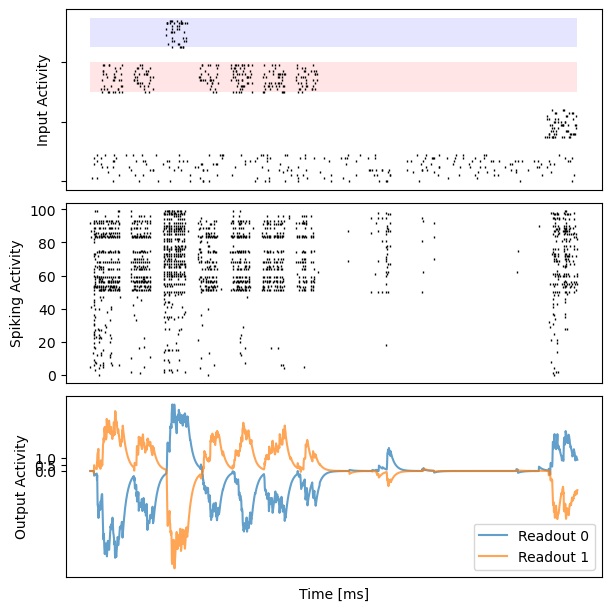
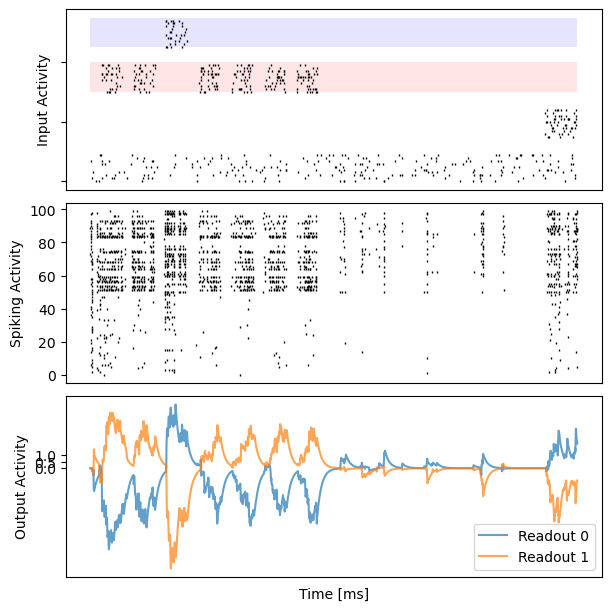
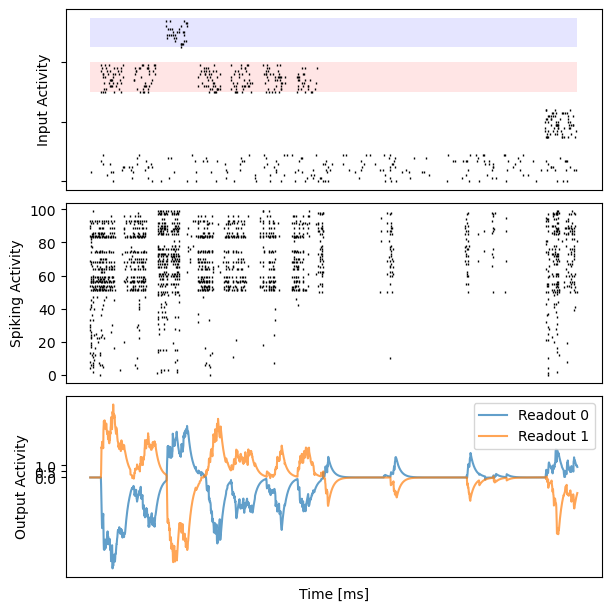
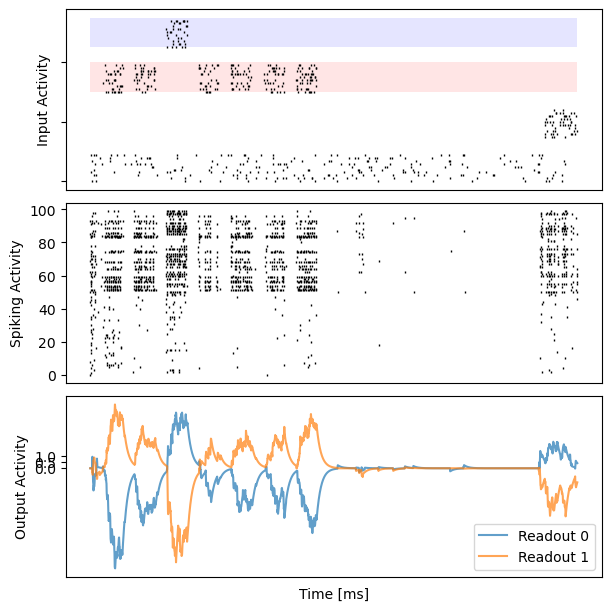
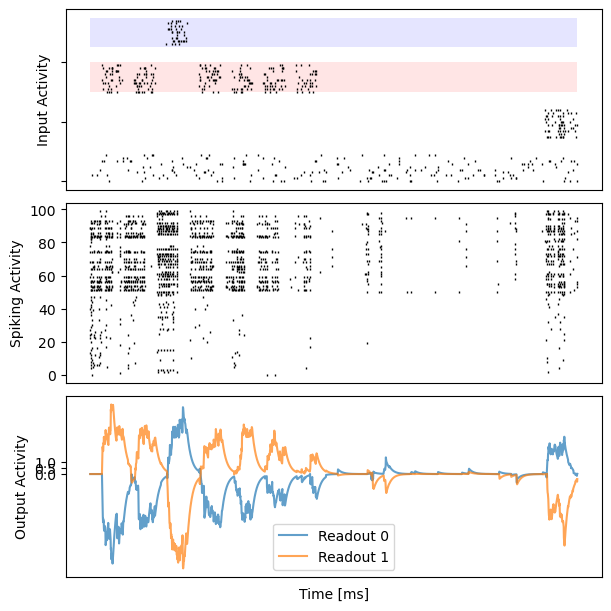
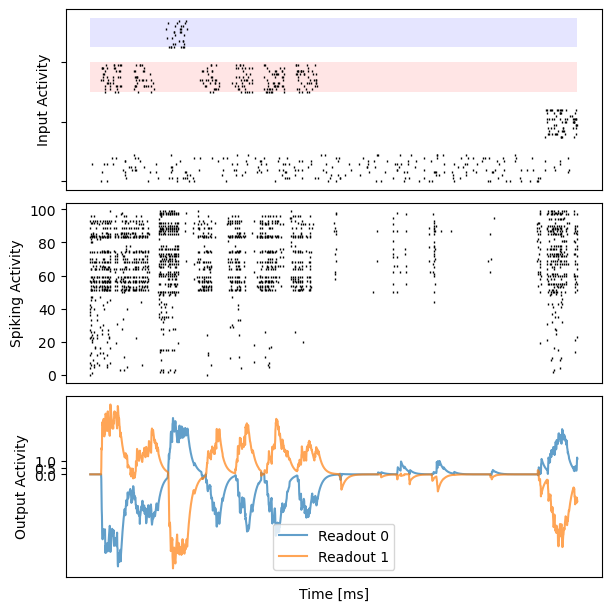
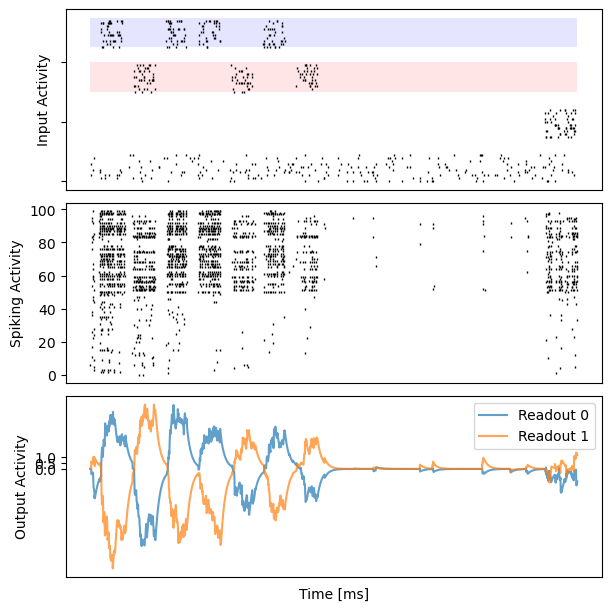
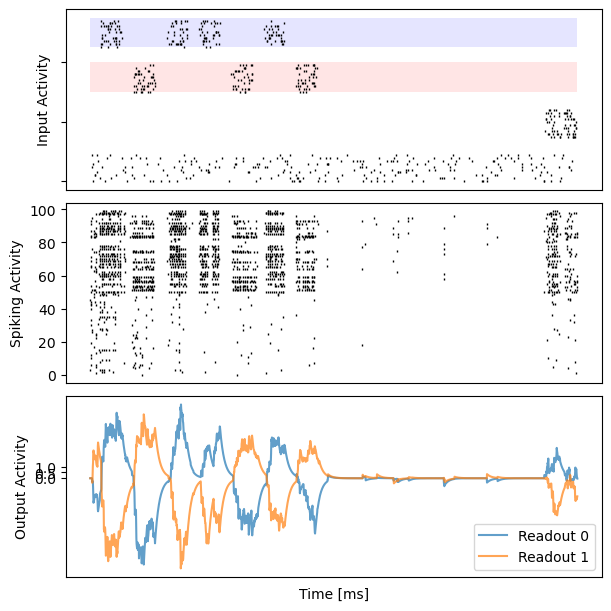
# visualization
dataset, _ = next(get_data(20, n_in=net.num_in, t_interval=t_cue_spacing, f0=input_f0)())
runner = bp.DSTrainer(net, monitors={'spike': net.r.spike})
outs = runner.predict(dataset, reset_state=True)

for i in range(10):
  fig, gs = bp.visualize.get_figure(3, 1, 2., 6.)
  ax_inp = fig.add_subplot(gs[0, 0])
  ax_rec = fig.add_subplot(gs[1, 0])
  ax_out = fig.add_subplot(gs[2, 0])

  data = dataset[i]
  # insert empty row
  n_channel = data.shape[1] // 4
  zero_fill = np.zeros((data.shape[0], int(n_channel / 2)))
  data = np.concatenate((data[:, 3 * n_channel:], zero_fill,
                         data[:, 2 * n_channel:3 * n_channel], zero_fill,
                         data[:, :n_channel], zero_fill,
                         data[:, n_channel:2 * n_channel]), axis=1)
  ax_inp.set_yticklabels([])
  ax_inp.add_patch(patches.Rectangle((0, 2 * n_channel + 2 * int(n_channel / 2)),
                                     data.shape[0], n_channel,
                                     facecolor="red", alpha=0.1))
  ax_inp.add_patch(patches.Rectangle((0, 3 * n_channel + 3 * int(n_channel / 2)),
                                     data.shape[0], n_channel,
                                     facecolor="blue", alpha=0.1))
  bp.visualize.raster_plot(runner.mon.ts, data, ax=ax_inp, marker='|')
  ax_inp.set_ylabel('Input Activity')
  ax_inp.set_xticklabels([])
  ax_inp.set_xticks([])

  # spiking activity
  bp.visualize.raster_plot(runner.mon.ts, runner.mon['spike'][i], ax=ax_rec, marker='|')
  ax_rec.set_ylabel('Spiking Activity')
  ax_rec.set_xticklabels([])
  ax_rec.set_xticks([])
  # decision activity
  ax_out.set_yticks([0, 0.5, 1])
  ax_out.set_ylabel('Output Activity')
  ax_out.plot(runner.mon.ts, outs[i, :, 0], label='Readout 0', alpha=0.7)
  ax_out.plot(runner.mon.ts, outs[i, :, 1], label='Readout 1', alpha=0.7)
  ax_out.set_xticklabels([])
  ax_out.set_xticks([])
  ax_out.set_xlabel('Time [ms]')
  plt.legend()
  plt.show()