(Bouchacourt & Buschman, 2019) Flexible Working Memory Model
Implementation of :
Bouchacourt, Flora, and Timothy J. Buschman. “A flexible model of working memory.” Neuron 103.1 (2019): 147-160.
Author:
Chaoming Wang (chao.brain@qq.com)
[1]:
import matplotlib.pyplot as plt
import jax
[2]:
import brainpy as bp
import brainpy.math as bm
[3]:
bp.__version__
[3]:
'2.4.3'
[4]:
# increase in order to run multiple trials with the same network
num_trials = 1
num_item_to_load = 6
[5]:
# Parameters for network architecture
# ------------------------------------
num_sensory_neuron = 512 # Number of recurrent neurons per sensory network
num_sensory_pool = 8 # Number of ring-like sensory network
num_all_sensory = num_sensory_pool * num_sensory_neuron
num_all_random = 1024 # Number of neuron in the random network
fI_slope = 0.4 # slope of the non-linear f-I function
bias = 0. # bias in the neuron firing response (cf page 1 right column of Burak, Fiete 2012)
tau = 10. # Synaptic time constant [ms]
init_range = 0.01 # Range to randomly initialize synaptic variables
[6]:
# Parameters for sensory network
# -------------------------------
k2 = 0.25 # width of negative surround suppression
k1 = 1. # width of positive amplification
A = 2. # amplitude of weight function
lambda_ = 0.28 # baseline of weight matrix for recurrent network
[7]:
# Parameters for interaction of
# random network <-> sensory network
# -----------------------------------
forward_balance = -1. # if -1, perfect feed-forward balance from SN to RN
backward_balance = -1. # if -1, perfect feedback balance from RN to SN
alpha = 2.1 # parameter used to compute the feedforward weight, before balancing
beta = 0.2 # parameter used to compute the feedback weight, before balancing
gamma = 0.35 # connectivity (gamma in the paper)
factor = 1000 # factor for computing weights values
[8]:
# Parameters for stimulus
# -----------------------
simulation_time = 1100 # # the simulation time [ms]
start_stimulation = 100 # [ms]
end_stimulation = 200 # [ms]
input_strength = 10 # strength of the stimulation
num_sensory_input_width = 32
# the width for input stimulation of the gaussian distribution
sigma = round(num_sensory_neuron / num_sensory_input_width)
three_sigma = 3 * sigma
activity_threshold = 3
[9]:
# Weights initialization
# ----------------------
# weight matrix within sensory network
sensory_encoding = 2. * bm.pi * bm.arange(1, num_sensory_neuron + 1) / num_sensory_neuron
diff = sensory_encoding.reshape((-1, 1)) - sensory_encoding
weight_mat_of_sensory = lambda_ + A * bm.exp(k1 * (bm.cos(diff) - 1)) - A * bm.exp(k2 * (bm.cos(diff) - 1))
diag = bm.arange(num_sensory_neuron)
weight_mat_of_sensory[diag, diag] = 0.
No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.)
[10]:
# connectivity matrix between sensory and random network
conn_matrix_sensory2random = bm.random.rand(num_all_sensory, num_all_random) < gamma
[11]:
# weight matrix of sensory2random
ws = factor * alpha / conn_matrix_sensory2random.sum(axis=0)
weight_mat_sensory2random = conn_matrix_sensory2random * ws.reshape((1, -1))
ws = weight_mat_sensory2random.sum(axis=0).reshape((1, -1))
weight_mat_sensory2random += forward_balance / num_all_sensory * ws # balance
[12]:
# weight matrix of random2sensory
ws = factor * beta / conn_matrix_sensory2random.sum(axis=1)
weight_mat_random2sensory = conn_matrix_sensory2random.T * ws.reshape((1, -1))
ws = weight_mat_random2sensory.sum(axis=0).reshape((1, -1))
weight_mat_random2sensory += backward_balance / num_all_random * ws # balance
[13]:
@jax.jit
def f(inp_ids, center):
inp_scale = bm.exp(-(inp_ids - center) ** 2 / 2 / sigma ** 2) / (bm.sqrt(2 * bm.pi) * sigma)
inp_scale /= bm.max(inp_scale)
inp_ids = bm.remainder(inp_ids - 1, num_sensory_neuron)
input = bm.zeros(num_sensory_neuron)
input[inp_ids] = input_strength * inp_scale
input -= bm.sum(input) / num_sensory_neuron
return input
def get_input(center):
inp_ids = bm.arange(bm.asarray(center - three_sigma, dtype=bm.int32),
bm.asarray(center + three_sigma + 1, dtype=bm.int32),
1)
return f(inp_ids, center)
[14]:
def get_activity_vector(rates):
exp_stim_encoding = bm.exp(1j * sensory_encoding)
timed_abs = bm.zeros(num_sensory_pool)
timed_angle = bm.zeros(num_sensory_pool)
for si in range(num_sensory_pool):
start = si * num_sensory_neuron
end = (si + 1) * num_sensory_neuron
exp_rates = bm.multiply(rates[start:end], exp_stim_encoding)
mean_rates = bm.mean(exp_rates)
timed_angle[si] = bm.angle(mean_rates) * num_sensory_neuron / (2 * bm.pi)
timed_abs[si] = bm.absolute(mean_rates)
timed_angle[timed_angle < 0] += num_sensory_neuron
return timed_abs, timed_angle
[15]:
class PoissonNeuron(bp.NeuGroup):
def __init__(self, size, **kwargs):
super().__init__(size=size, **kwargs)
self.s = bm.Variable(bm.zeros(self.num))
self.r = bm.Variable(bm.zeros(self.num))
self.input = bm.Variable(bm.zeros(self.num))
self.spike = bm.Variable(bm.zeros(self.num, dtype=bool))
self.rng = bm.random.RandomState()
self.int_s = bp.odeint(lambda s, t: -s / tau, method='exp_euler')
def update(self):
tdi = bp.share.get_shargs()
self.s.value = self.int_s(self.s, tdi.t, tdi.dt)
self.r.value = 0.4 * (1. + bm.tanh(fI_slope * (self.input + self.s + bias) - 3.)) / tau
self.spike.value = self.rng.random(self.s.shape) < self.r * tdi.dt
self.input[:] = 0.
def reset_state(self, batch_size=None):
self.s.value = self.rng.random(self.num) * init_range
self.r.value = 0.4 * (1. + bm.tanh(fI_slope * (bias + self.s) - 3.)) / tau
self.input.value = bm.zeros(self.num)
self.spike.value = bm.zeros(self.num, dtype=bool)
[16]:
class Sen2SenSyn(bp.SynConn):
def __init__(self, pre, post, **kwargs):
super(Sen2SenSyn, self).__init__(pre=pre, post=post, **kwargs)
def update(self):
for i in range(num_sensory_pool):
start = i * num_sensory_neuron
end = (i + 1) * num_sensory_neuron
self.post.s[start: end] += bm.dot(self.pre.spike[start: end],
weight_mat_of_sensory)
d:\codes\projects\brainpy\brainpy\_src\deprecations.py:86: DeprecationWarning: brainpy.SynConn is deprecated. Use brainpy.dyn.SynConn instead.
_deprecate(message)
[17]:
class OtherSyn(bp.SynConn):
def __init__(self, pre, post, weights, **kwargs):
super(OtherSyn, self).__init__(pre=pre, post=post, **kwargs)
self.weights = weights
def update(self):
self.post.s += bm.dot(self.pre.spike, self.weights)
d:\codes\projects\brainpy\brainpy\_src\deprecations.py:86: DeprecationWarning: brainpy.SynConn is deprecated. Use brainpy.dyn.SynConn instead.
_deprecate(message)
[18]:
class Network(bp.DynSysGroup):
def __init__(self):
super().__init__()
self.sensory = PoissonNeuron(num_all_sensory)
self.random = PoissonNeuron(num_all_random)
self.sensory2sensory = Sen2SenSyn(pre=self.sensory, post=self.sensory)
self.random2sensory = OtherSyn(pre=self.random,
post=self.sensory,
weights=weight_mat_random2sensory)
self.sensory2random = OtherSyn(pre=self.sensory,
post=self.random,
weights=weight_mat_sensory2random)
[19]:
for trial_idx in range(num_trials):
# inputs
# ------
pools_receiving_inputs = bm.random.choice(num_sensory_pool, num_item_to_load, replace=False)
print(f"Load {num_item_to_load} items in trial {trial_idx}.\n")
input_center = bm.ones(num_sensory_pool) * num_sensory_neuron / 2
inp_vector = bm.zeros((num_sensory_pool, num_sensory_neuron))
for si in pools_receiving_inputs:
inp_vector[si, :] = get_input(input_center[si])
inp_vector = inp_vector.flatten()
Iext, duration = bp.inputs.constant_input(
[(0., start_stimulation),
(inp_vector, end_stimulation - start_stimulation),
(0., simulation_time - end_stimulation)]
)
# running
# -------
net = Network()
runner = bp.DSRunner(net,
inputs=(net.sensory.input, Iext, 'iter'),
monitors={'S.r': net.sensory.r,
'S.spike': net.sensory.spike,
'R.spike': net.random.spike})
runner.predict(duration, reset_state=True)
# results
# --------
rate_abs, rate_angle = get_activity_vector(runner.mon['S.r'][-1] * 1e3)
print(f"Stimulus is given in: {bm.sort(pools_receiving_inputs)}")
print(f"Memory is found in: {bm.where(rate_abs > activity_threshold)[0]}")
prob_maintained, prob_spurious = 0, 0
for si in range(num_sensory_pool):
if rate_abs[si] > activity_threshold:
if si in pools_receiving_inputs:
prob_maintained += 1
else:
prob_spurious += 1
print(str(prob_maintained) + ' maintained memories')
print(str(pools_receiving_inputs.shape[0] - prob_maintained) + ' forgotten memories')
print(str(prob_spurious) + ' spurious memories\n')
prob_maintained /= float(num_item_to_load)
if num_item_to_load != num_sensory_pool:
prob_spurious /= float(num_sensory_pool - num_item_to_load)
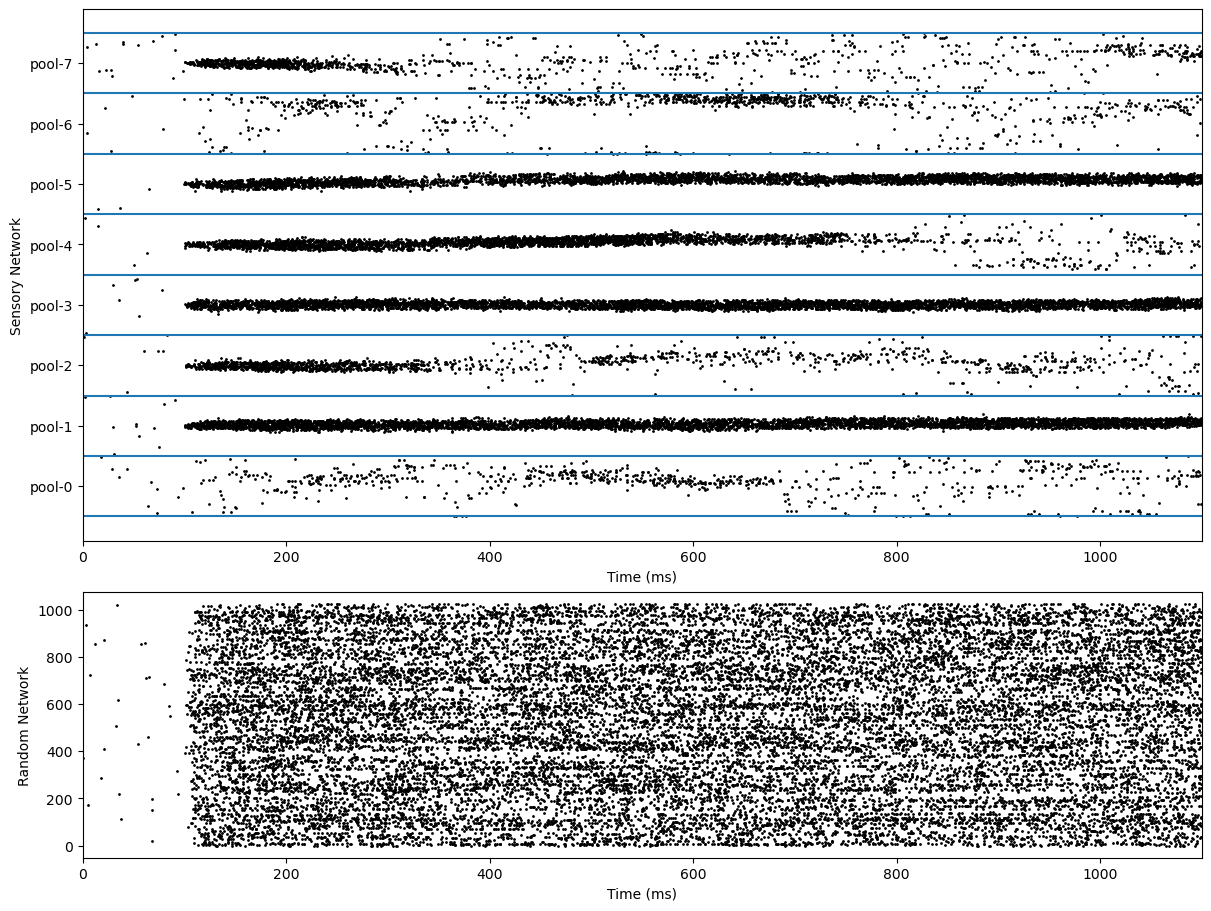
# visualization
# -------------
fig, gs = bp.visualize.get_figure(6, 1, 1.5, 12)
xlim = (0, duration)
fig.add_subplot(gs[0:4, 0])
bp.visualize.raster_plot(runner.mon.ts,
runner.mon['S.spike'],
ylabel='Sensory Network', xlim=xlim)
for index_sn in range(num_sensory_pool + 1):
plt.axhline(index_sn * num_sensory_neuron)
plt.yticks([num_sensory_neuron * (i + 0.5) for i in range(num_sensory_pool)],
[f'pool-{i}' for i in range(num_sensory_pool)])
fig.add_subplot(gs[4:6, 0])
bp.visualize.raster_plot(runner.mon.ts,
runner.mon['R.spike'],
ylabel='Random Network', xlim=xlim, show=True)
Load 6 items in trial 0.
Stimulus is given in: [1 2 3 4 5 7]
Memory is found in: [1 3 5]
3 maintained memories
3 forgotten memories
0 spurious memories