(Si Wu, 2008): Continuous-attractor Neural Network 2D
Implementation of the paper: - Si Wu, Kosuke Hamaguchi, and Shun-ichi Amari. “Dynamics and computation of continuous attractors.” Neural computation 20.4 (2008): 994-1025.
The mathematical equation of the Continuous-Attractor Neural Network (CANN) is given by:
\[\tau \frac{du(x,t)}{dt} = -u(x,t) + \rho \int dx' J(x,x') r(x',t)+I_{ext}\]
\[r(x,t) = \frac{u(x,t)^2}{1 + k \rho \int dx' u(x',t)^2}\]
\[J(x,x') = \frac{1}{\sqrt{2\pi}a}\exp(-\frac{|x-x'|^2}{2a^2})\]
\[I_{ext} = A\exp\left[-\frac{|x-z(t)|^2}{4a^2}\right]\]
The model solving is usig Fast Fourier transform. It can run on CPU, GPU, TPU devices.
[1]:
import matplotlib.pyplot as plt
import numpy as np
import jax
[2]:
import brainpy as bp
import brainpy.math as bm
[5]:
class CANN2D(bp.dyn.NeuGroup):
def __init__(self, length, tau=1., k=8.1, a=0.5, A=10., J0=4.,
z_min=-bm.pi, z_max=bm.pi, name=None):
super(CANN2D, self).__init__(size=(length, length), name=name)
# parameters
self.length = length
self.tau = tau # The synaptic time constant
self.k = k # Degree of the rescaled inhibition
self.a = a # Half-width of the range of excitatory connections
self.A = A # Magnitude of the external input
self.J0 = J0 # maximum connection value
# feature space
self.z_min = z_min
self.z_max = z_max
self.z_range = z_max - z_min
self.x = bm.linspace(z_min, z_max, length) # The encoded feature values
self.rho = length / self.z_range # The neural density
self.dx = self.z_range / length # The stimulus density
# The connections
self.conn_mat = self.make_conn()
# variables
self.r = bm.Variable(bm.zeros((length, length)))
self.u = bm.Variable(bm.zeros((length, length)))
self.input = bm.Variable(bm.zeros((length, length)))
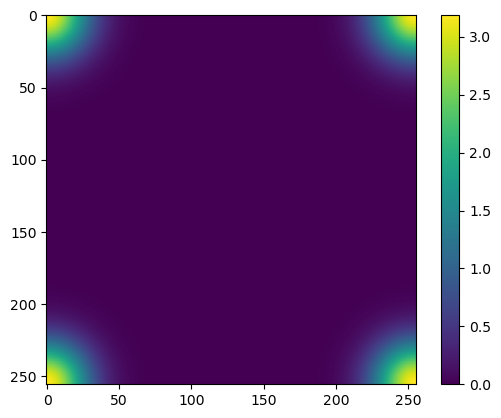
def show_conn(self):
plt.imshow(np.asarray(self.conn_mat))
plt.colorbar()
plt.show()
def dist(self, d):
v_size = bm.asarray([self.z_range, self.z_range])
return bm.where(d > v_size / 2, v_size - d, d)
def make_conn(self):
x1, x2 = bm.meshgrid(self.x, self.x)
value = bm.stack([x1.flatten(), x2.flatten()]).T
d = self.dist(bm.abs(value[0] - value))
d = bm.linalg.norm(d, axis=1)
d = d.reshape((self.length, self.length))
Jxx = self.J0 * bm.exp(-0.5 * bm.square(d / self.a)) / (bm.sqrt(2 * bm.pi) * self.a)
return Jxx
def get_stimulus_by_pos(self, pos):
assert bm.size(pos) == 2
x1, x2 = bm.meshgrid(self.x, self.x)
value = bm.stack([x1.flatten(), x2.flatten()]).T
d = self.dist(bm.abs(bm.asarray(pos) - value))
d = bm.linalg.norm(d, axis=1)
d = d.reshape((self.length, self.length))
return self.A * bm.exp(-0.25 * bm.square(d / self.a))
def update(self, _t, _dt):
r1 = bm.square(self.u)
r2 = 1.0 + self.k * bm.sum(r1)
self.r.value = r1 / r2
r = bm.fft.fft2(self.r)
jjft = bm.fft.fft2(self.conn_mat)
interaction = bm.real(bm.fft.ifft2(r * jjft))
self.u.value = self.u + (-self.u + self.input + interaction) / self.tau * _dt
self.input[:] = 0.
[6]:
cann = CANN2D(length=256, k=0.1)
[7]:
cann.show_conn()
[8]:
# encoding
Iext, length = bp.inputs.section_input(
values=[cann.get_stimulus_by_pos([0., 0.]), 0.],
durations=[10., 20.],
return_length=True
)
runner = bp.dyn.DSRunner(cann,
inputs=['input', Iext, 'iter'],
monitors=['r'],
dyn_vars=cann.vars())
runner.run(length)
[8]:
2.7321479320526123
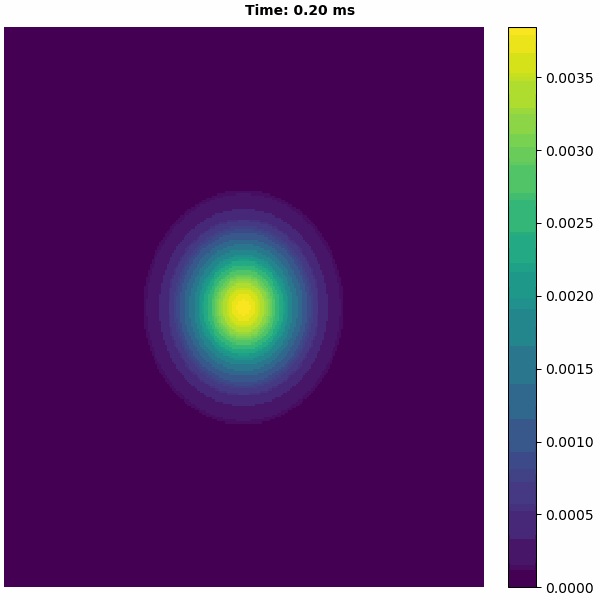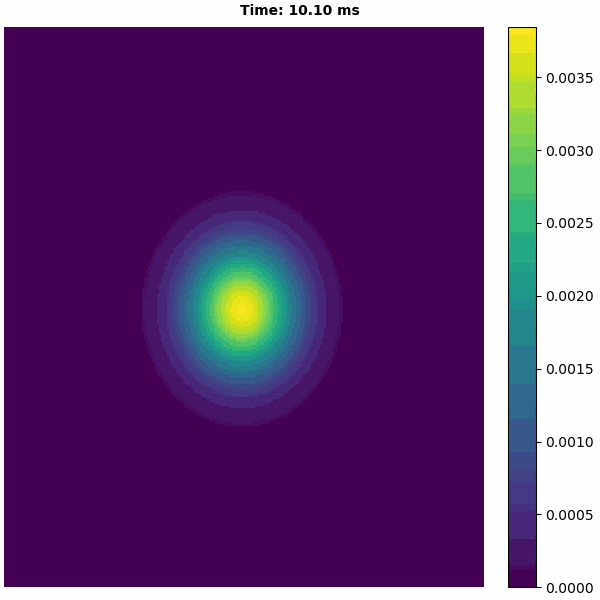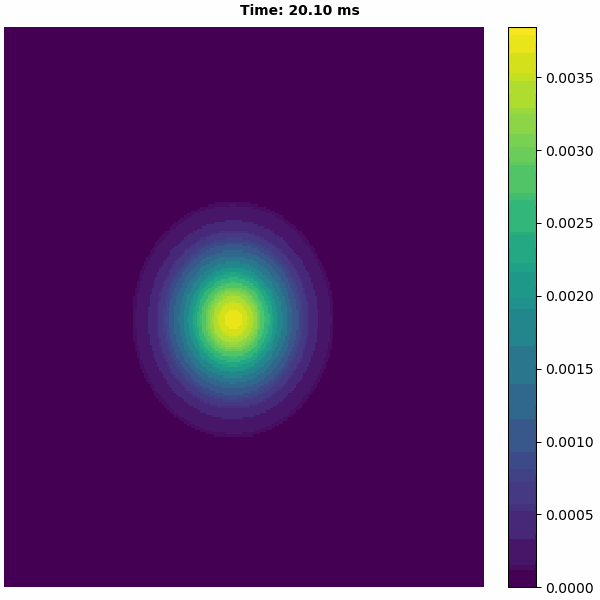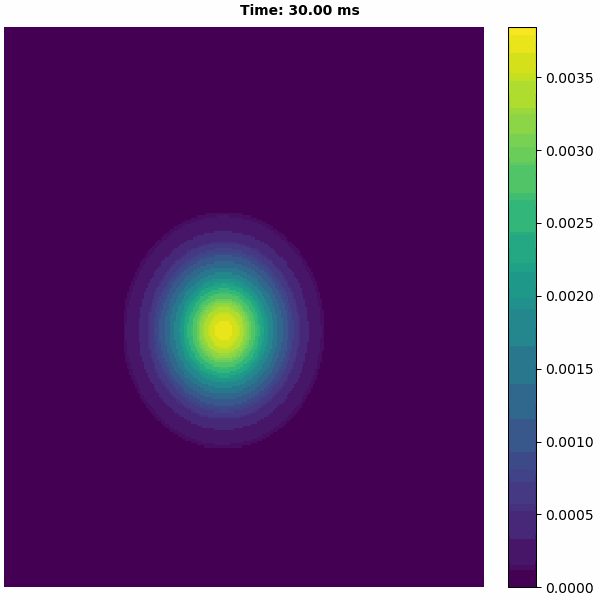
[9]:
bp.visualize.animate_2D(values=runner.mon.r,
net_size=(cann.length, cann.length),
show=False)
[9]:
<matplotlib.animation.FuncAnimation at 0x239bee9dac8>
[10]:
# tracking
length = 20
positions = bp.inputs.ramp_input(-bm.pi, bm.pi, duration=length, t_start=0)
positions = bm.stack([positions, positions]).T
Iext = jax.vmap(cann.get_stimulus_by_pos)(positions)
runner = bp.dyn.DSRunner(cann,
inputs=['input', Iext, 'iter'],
monitors=['r'],
dyn_vars=cann.vars())
runner.run(length)
[10]:
2.339928150177002
[11]:
bp.visualize.animate_2D(values=runner.mon.r,
net_size=(cann.length, cann.length),
show=False)
[11]:
<matplotlib.animation.FuncAnimation at 0x239c40c5e10>
![]()