Fractional-order Chaos Gallery
[1]:
import brainpy as bp
import matplotlib.pyplot as plt
[2]:
def plot_runner_3d(runner):
fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(111, projection='3d')
plt.plot(runner.mon.x.flatten(),
runner.mon.y.flatten(),
runner.mon.z.flatten())
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
plt.show()
[3]:
def plot_runner_2d(runner):
plt.figure(figsize=(12, 6))
plt.subplot(121)
plt.plot(runner.mon.x.flatten(), runner.mon.y.flatten())
plt.xlabel('x')
plt.ylabel('y')
plt.subplot(122)
plt.plot(runner.mon.x.flatten(), runner.mon.z.flatten())
plt.xlabel('x')
plt.ylabel('z')
plt.show()
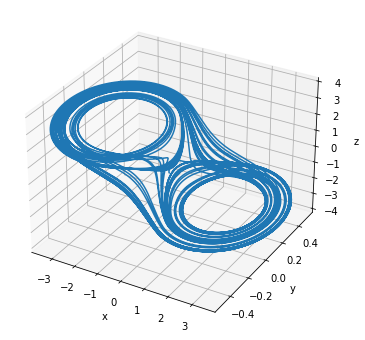
Fractional-order Chua system
The fractional-order Chua’s system is given by [1]
\[\begin{split}\left\{\begin{array}{l}
D^{\alpha_{1}} x=a\{y- (1+m_1) x-0.5*(m_0-m_1)*(|x+1|-|x-1|)\} \\
D^{\alpha_{2}} y=x-y+z \\
D^{\alpha_{3}} z=-b y-c z
\end{array}\right.\end{split}\]
[4]:
a, b, c = 10.725, 10.593, 0.268
m0, m1 = -1.1726, -0.7872
def chua_system(x, y, z, t):
f = m1*x+0.5*(m0-m1)*(abs(x+1)-abs(x-1))
dx = a*(y-x-f)
dy = x - y + z
dz = -b*y - c*z
return dx, dy, dz
[5]:
dt = 0.001
duration = 200
inits = [0.2, -0.1, 0.1]
integrator = bp.fde.GLShortMemory(chua_system,
alpha=[0.93, 0.99, 0.92],
num_memory=1000,
inits=inits)
runner = bp.integrators.IntegratorRunner(integrator,
monitors=list('xyz'),
inits=inits,
dt=dt)
runner.run(duration)
WARNING:absl:No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.)
[6]:
plot_runner_3d(runner)
[7]:
plot_runner_2d(runner)
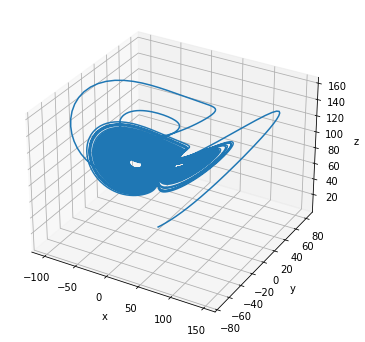
Fractional-order Qi System
The fractional-order Qi chaotic system is given by
\[\begin{split}\left\{\begin{array}{l}
D^{\alpha} x_{1}=a\left(x_{1}-x_{2}\right)+x_{2} x_{3} \\
D^{\alpha} x_{2}=c x_{1}-x_{2}-x_{1} x_{3} \\
D^{\alpha} x_{3}=x_{1} x_{2}-b x_{3}
\end{array}\right.\end{split}\]
[8]:
a, b, c = 35, 8/3, 80
def qi_system(x, y, z, t):
dx = -a*x + a*y + y*z
dy = c*x - y - x*z
dz = -b*z + x*y
return dx, dy, dz
[9]:
dt = 0.001
duration = 200
inits = [0.1, 0.2, 0.3]
integrator = bp.fde.GLShortMemory(qi_system,
alpha=0.98,
num_memory=1000,
inits=inits)
runner = bp.integrators.IntegratorRunner(integrator,
monitors=list('xyz'),
inits=inits,
dt=dt)
runner.run(duration)
[10]:
plot_runner_3d(runner)
[11]:
plot_runner_2d(runner)
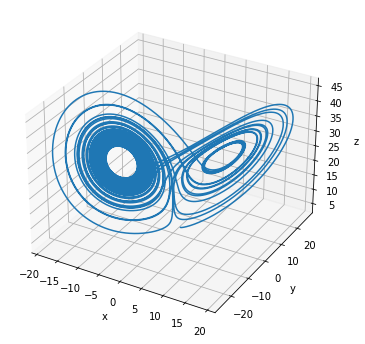
Fractional-order Lorenz System
The fractional-order Lorenz system is given by [3]
\[\begin{split}\left\{\begin{array}{l}
D^{\alpha} x=a\left(y-x\right) \\
D^{\alpha} y= x * (b - z) - y \\
D^{\alpha} z =x * y - c * z
\end{array}\right.\end{split}\]
[12]:
a, b, c = 10, 28, 8 / 3
def lorenz_system(x, y, z, t):
dx = a * (y - x)
dy = x * (b - z) - y
dz = x * y - c * z
return dx, dy, dz
[13]:
dt = 0.001
duration = 50
inits = [1, 2, 3]
integrator = bp.fde.GLShortMemory(lorenz_system,
alpha=0.99, # fractional order
num_memory=1000,
inits=inits)
runner = bp.integrators.IntegratorRunner(integrator,
monitors=list('xyz'),
inits=inits,
dt=dt)
runner.run(duration)
[14]:
plot_runner_3d(runner)
[15]:
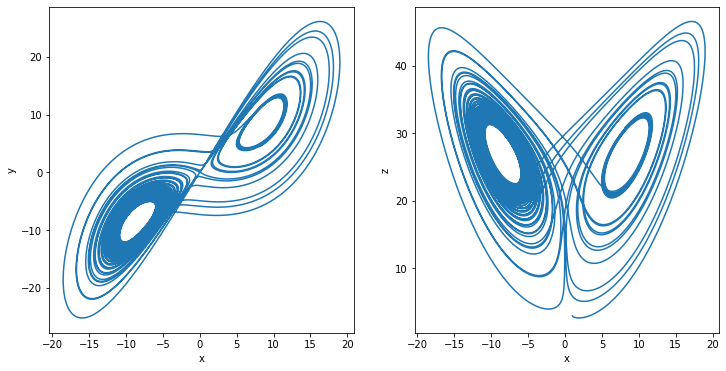
plot_runner_2d(runner)
Fractional-order Liu System
The fractional order system is given by [4]
\[\begin{split}\begin{aligned}
&D^{\alpha_{1}} x=-a x-e y^{2} \\
&D^{\alpha_{2}} y=b y-n x z \\
&D^{\alpha_{3}} z=-c z+m x y
\end{aligned}\end{split}\]
[16]:
a, b, c, e, n, m = 1, 2.5, 5, 1, 4, 4
def liu_system(x, y, z, t):
dx = -a*x-e*y**2
dy = b*y-n*x*z
dz = -c*z+m*x*y
return dx, dy, dz
[17]:
dt = 0.001
duration = 100
inits = [0.2, 0, 0.5]
integrator = bp.fde.GLShortMemory(liu_system,
alpha=0.95, # fractional order
num_memory=1000,
inits=inits)
runner = bp.integrators.IntegratorRunner(integrator,
monitors=list('xyz'),
inits=inits,
dt=dt)
runner.run(duration)
[18]:
plot_runner_3d(runner)
[19]:
plot_runner_2d(runner)
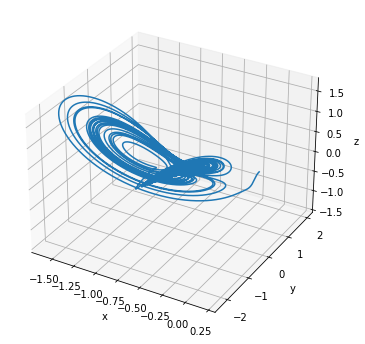
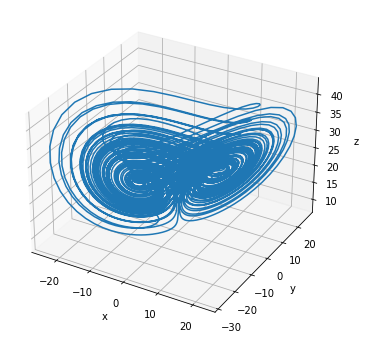
Fractional-order Chen System
The system is given by [5]
\[\begin{split}\begin{aligned}
&\frac{\mathrm{d}^{q} x}{\mathrm{~d} t^{9}}=a(y-x), \\
&\frac{\mathrm{d}^{q} y}{\mathrm{~d} t^{q}}= d x-x z+c y, \\
&\frac{\mathrm{d}^{q} z}{\mathrm{~d} t^{9}}=x y-b z,
\end{aligned}\end{split}\]
[20]:
a, b, c, d = 35, 3, 28, -7
def chen_system(x, y, z, t):
dx = a*(y-x)
dy = d*x-x*z+c*y
dz = x*y-b*z
return dx, dy, dz
[21]:
dt = 0.005
duration = 50
inits = [-9, -5, 14]
integrator = bp.fde.GLShortMemory(chen_system,
alpha=0.9, # fractional order
num_memory=1000,
inits=inits)
runner = bp.integrators.IntegratorRunner(integrator,
monitors=list('xyz'),
inits=inits,
dt=dt)
runner.run(duration)
[22]:
plot_runner_3d(runner)
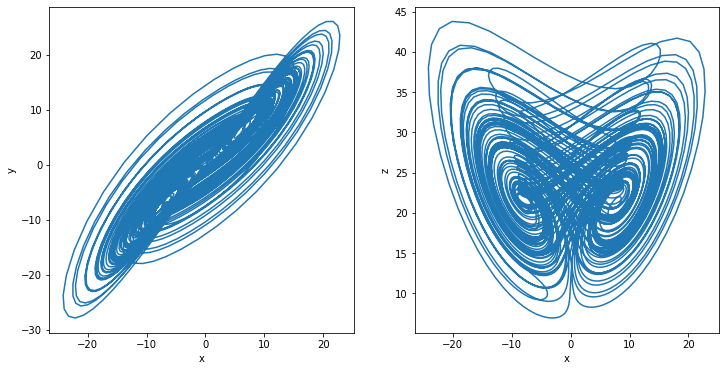
[23]:
plot_runner_2d(runner)
References
[1] Petráš, Ivo. “A note on the fractional-order Chua’s system.” Chaos, Solitons & Fractals 38.1 (2008): 140-147.
[2] Wu, Xiangjun, and Yang Yang. “Chaos in the fractional-order Qi system and its synchronization using active control.” 2010 International Conference on Intelligent Computing and Cognitive Informatics. IEEE, 2010.
[3] Wu, Xiang-Jun, and Shi-Lei Shen. “Chaos in the fractional-order Lorenz system.” International Journal of Computer Mathematics 86.7 (2009): 1274-1282.
[4] Daftardar-Gejji, Varsha, and Sachin Bhalekar. “Chaos in fractional ordered Liu system.” Computers & mathematics with applications 59.3 (2010): 1117-1127.
[5] Lu, Jun Guo, and Guanrong Chen. “A note on the fractional-order Chen system.” Chaos, Solitons & Fractals 27.3 (2006): 685-688.