(Wang, 2002) Decision making spiking model
Implementation of the paper: Wang, Xiao-Jing. “Probabilistic decision making by slow reverberation in cortical circuits.” Neuron 36.5 (2002): 955-968.
Author : Chaoming Wang (chao.brain@qq.com)
[1]:
import brainpy as bp
import brainpy.math as bm
import matplotlib.pyplot as plt
bm.use_backend('jax')
WARNING:absl:No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.)
Neuron model
LIF neurons
Both pyramidal cells and interneurons are described by leaky integrate-and-fire neurons.
\[C_{m} \frac{d V(t)}{d t}=-g_{L}\left(V(t)-V_{L}\right)-I_{s y n}(t)\]
where
\(I_{syn}(t)\) represents the total synaptic current flowing into the cell
resting potential \(V_L\) = -70 mV
firing threshold \(V_{th}\) = -50 mV
reset potential \(V_{rest}\) = -55 mV
membrane capacitance \(C_m\) = 0.5 nF for pyramidal cells and 0.2 nF for interneurons
membrane leak conductance \(g_L\) = 25 nS for pyramidal cells and 20 nS for interneurons
refractory period \(\tau_{ref}\) = 2 ms for pyramidal cells and 1 ms for interneurons
[2]:
class LIF(bp.NeuGroup):
def __init__(self, size, V_L=-70., V_reset=-55., V_th=-50.,
Cm=0.5, gL=0.025, t_refractory=2., **kwargs):
super(LIF, self).__init__(size=size, **kwargs)
self.V_L = V_L
self.V_reset = V_reset
self.V_th = V_th
self.Cm = Cm
self.gL = gL
self.t_refractory = t_refractory
self.V = bm.Variable(bm.ones(self.num) * V_L)
self.input = bm.Variable(bm.zeros(self.num))
self.spike = bm.Variable(bm.zeros(self.num, dtype=bool))
self.refractory = bm.Variable(bm.zeros(self.num, dtype=bool))
self.t_last_spike = bm.Variable(bm.ones(self.num) * -1e7)
self.integral = bp.odeint(self.derivative)
def derivative(self, V, t, Iext):
dVdt = (- self.gL * (V - self.V_L) - Iext) / self.Cm
return dVdt
def update(self, _t, _dt):
ref = (_t - self.t_last_spike) <= self.t_refractory
V = self.integral(self.V, _t, self.input)
V = bm.where(ref, self.V, V)
spike = (V >= self.V_th)
self.V.value = bm.where(spike, self.V_reset, V)
self.spike.value = spike
self.t_last_spike.value = bm.where(spike, _t, self.t_last_spike)
self.refractory.value = bm.logical_or(spike, ref)
self.input[:] = 0.
Poisson neurons
[3]:
class PoissonNoise(bp.NeuGroup):
def __init__(self, size, freq, **kwargs):
super(PoissonNoise, self).__init__(size=size, **kwargs)
self.freq = bm.Variable(bm.array([freq]))
self.dt = bm.get_dt() / 1000.
self.spike = bm.Variable(bm.zeros(self.num, dtype=bool))
self.rng = bm.random.RandomState()
def update(self, _t, _dt):
self.spike.value = self.rng.random(self.num) < self.freq[0] * self.dt
[4]:
class PoissonStim(bp.NeuGroup):
def __init__(self, size, freq_mean, freq_var, t_interval, **kwargs):
super(PoissonStim, self).__init__(size=size, **kwargs)
self.freq_mean = freq_mean
self.freq_var = freq_var
self.t_interval = t_interval
self.dt = bm.get_dt() / 1000.
self.freq = bm.Variable(bm.zeros(1))
self.freq_t_last_change = bm.Variable(bm.ones(1) * -1e7)
self.spike = bm.Variable(bm.zeros(self.num, dtype=bool))
self.rng = bm.random.RandomState()
def update(self, _t, _dt):
in_interval = bm.logical_and(pre_period < _t, _t < pre_period + stim_period)
prev_freq = bm.where(in_interval, self.freq[0], 0.)
in_interval = bm.logical_and(in_interval, (_t - self.freq_t_last_change[0]) >= self.t_interval)
self.freq[:] = bm.where(in_interval, self.rng.normal(self.freq_mean, self.freq_var), prev_freq)
self.freq_t_last_change[:] = bm.where(in_interval, _t, self.freq_t_last_change[0])
self.spike.value = self.rng.random(self.num) < self.freq[0] * self.dt
Synapse models
The total synaptic currents are given by
\[I_{s y n}(t)=I_{e x t, A M P A}(t)+I_{r e c, A M P A}(t)+I_{r e c, N M D A}(t)+I_{r e c, G A B A}(t)\]
in which
\[\begin{split}\begin{gathered}
I_{\mathrm{ext}, \mathrm{AMPA}}(t)=g_{\mathrm{ext}, \mathrm{AMPA}}\left(V(t)-V_{E}\right) \mathrm{s}^{\mathrm{ext}, \mathrm{AMPA}}(t) \\
I_{\mathrm{rec}, \mathrm{AMPA}}(t)=g_{\mathrm{rec}, \mathrm{AMPA}}\left(V(t)-V_{E}\right) \sum_{\mathrm{j}=1}^{\mathrm{C}_{\mathrm{E}}} W_{j} S_{j}^{\mathrm{AMPA}}(t) \\
I_{\mathrm{rec}, \mathrm{NMDA}}(t)=\frac{g_{\mathrm{NMDA}}\left(V(t)-V_{E}\right)}{\left(1+\left[\mathrm{Mg}^{2+}\right] \exp (-0.062 V(t)) / 3.57\right)} \sum_{j=1}^{\mathrm{c}_{E}} w_{j} \mathrm{~s}_{j}^{\mathrm{NMDA}}(t) \\
I_{\mathrm{rec}, \mathrm{GABA}}(t)=g_{\mathrm{GABA}}\left(V(t)-V_{l}\right) \sum_{j=1}^{c_{1}} s_{j}^{\mathrm{GABA}}(t)
\end{gathered}\end{split}\]
where
\(V_E\) = 0 mV
\(V_I\) = -70 mV
\(\left[\mathrm{Mg}^{2+}\right]\) = 1 mM
The dimensionless weights \(w_j\) represent the structured excitatory recurrent connections
the sum over \(j\) represents a sum over the synapses formed by presynaptic neurons \(j\)
AMPA
The AMPA (external and recurrent) channels are described by
\[\frac{d s_{j}^{A M P A}(t)}{d t}=-\frac{s_{j}^{A M P A}(t)}{\tau_{A M P A}}+\sum_{k} \delta\left(t-t_{j}^{k}\right)\]
where
the decay time of AMPA currents \(\tau_{A M P A}\) = 2 ms
for the external AMPA currents, the spikes are emitted according to a Poisson process with rate \(V_{ext}\) = 2400 Hz independently from cell to cell
[5]:
class AMPA_One(bp.TwoEndConn):
def __init__(self, pre, post, delay=0.5, g_max=0.10, E=0., tau=2.0, **kwargs):
super(AMPA_One, self).__init__(pre=pre, post=post, **kwargs)
# parameters
self.g_max = g_max
self.E = E
self.tau = tau
self.delay = delay
# variables
self.pre_spike = self.register_constant_delay('ps', size=self.pre.num, delay=delay)
self.s = bm.Variable(bm.zeros(self.pre.num))
# function
self.integral = bp.odeint(self.derivative)
def derivative(self, s, t):
ds = - s / self.tau
return ds
def update(self, _t, _dt):
self.pre_spike.push(self.pre.spike)
pre_spike = self.pre_spike.pull()
self.s.value = self.integral(self.s, _t)
self.s += pre_spike * self.g_max
self.post.input += self.s * (self.post.V - self.E)
[6]:
class AMPA(bp.TwoEndConn):
def __init__(self, pre, post, delay=0.5, g_max=0.10, E=0., tau=2.0, **kwargs):
super(AMPA, self).__init__(pre=pre, post=post, **kwargs)
# parameters
self.g_max = g_max
self.E = E
self.tau = tau
self.delay = delay
# variables
self.s = bm.Variable(bm.zeros(self.post.num))
self.pre_spike = self.register_constant_delay('ps', size=self.pre.num, delay=delay)
# function
self.integral = bp.odeint(self.derivative)
def derivative(self, s, t):
ds = - s / self.tau
return ds
def update(self, _t, _dt):
self.pre_spike.push(self.pre.spike)
pre_spike = self.pre_spike.pull()
self.s.value = self.integral(self.s, _t)
self.s += pre_spike.sum() * self.g_max
self.post.input += self.s * (self.post.V - self.E)
NMDA
NMDA channels are described by:
\[\begin{split}\begin{gathered}
\frac{d s_{j}^{\mathrm{NMDA}}(t)}{d t}=-\frac{s_{j}^{\mathrm{NMDA}}(t)}{\tau_{\mathrm{NMDA}, \text { decay }}}+\alpha x_{j}(t)\left(1-s_{j}^{\mathrm{NMDA}}(t)\right) \\
\frac{d x_{j}(t)}{d t}=-\frac{x_{j}(t)}{\tau_{\mathrm{NMDA}, \text { rise }}}+\sum_{k} \delta\left(t-t_{j}^{k}\right)
\end{gathered}\end{split}\]
where
the decay time \(\tau_{\mathrm{NMDA}, \text { decay }}\) = 100 ms
\(\alpha\) = 0.5 \(\mathrm{ms}^{-1}\)
the rise time \(\tau_{\mathrm{NMDA}, \text { rise }}\) = 2 ms
[7]:
class NMDA(bp.TwoEndConn):
def __init__(self, pre, post, delay=0.5, tau_decay=100, tau_rise=2.,
g_max=0.15, E=0., cc_Mg=1., alpha=0.5, **kwargs):
super(NMDA, self).__init__(pre=pre, post=post, **kwargs)
# parameters
self.g_max = g_max
self.E = E
self.cc_Mg = cc_Mg
self.alpha = alpha
self.tau_decay = tau_decay
self.tau_rise = tau_rise
self.delay = delay
self.size = (self.pre.num, self.post.num)
self.pre_one = bm.ones(self.pre.num)
# variables
self.pre_spike = self.register_constant_delay('ps', size=self.pre.num, delay=delay)
self.s = bm.Variable(bm.zeros(self.size))
self.x = bm.Variable(bm.zeros(self.size))
# function
self.integral = bp.odeint(self.derivative)
def derivative(self, s, x, t):
dsdt = -s / self.tau_decay + self.alpha * x * (1 - s)
dxdt = -x / self.tau_rise
return dsdt, dxdt
def update(self, _t, _dt):
self.pre_spike.push(self.pre.spike)
pre_spike = self.pre_spike.pull()
self.s.value, self.x.value = self.integral(self.s, self.x, _t)
self.x += pre_spike.reshape((-1, 1))
g_inf = 1 / (1 + self.cc_Mg * bm.exp(-0.062 * self.post.V) / 3.57)
Iext = bm.dot(self.pre_one, self.s) * (self.post.V - self.E) * g_inf
self.post.input += Iext * self.g_max
GABAA
The GABA synaptic variable obeys
\[\frac{d s_{j}^{G A B A}(t)}{d t}=-\frac{s_{j}^{G A B A}(t)}{\tau_{G A B A}}+\sum_{k} \delta\left(t-t_{j}^{k}\right)\]
where - the decay time of AMPA currents \(\tau_{GABA}\) = 5 ms
[8]:
class GABAa(AMPA):
def __init__(self, pre, post, delay=0.5, g_max=0.10, E=-70., tau=5.0, **kwargs):
super(GABAa, self).__init__(pre=pre, post=post, E=E, tau=tau, delay=delay, g_max=g_max, **kwargs)
Parameters
[9]:
scale = 1.
num_exc = int(1600 * scale)
num_inh = int(400 * scale)
f = 0.15
num_A = int(f * num_exc)
num_B = int(f * num_exc)
num_N = num_exc - num_A - num_B
print(f'Total network size: {num_exc + num_inh}')
Total network size: 2000
[10]:
mu0 = 40.
coherence = 25.6
[11]:
# times
pre_period = 100.
stim_period = 1000.
delay_period = 500.
total_period = pre_period + stim_period + delay_period
[12]:
poisson_freq = 2400. # Hz
w_pos = 1.7
w_neg = 1. - f * (w_pos - 1.) / (1. - f)
g_max_ext2E_AMPA = 2.1 * 1e-3 # uS
g_max_ext2I_AMPA = 1.62 * 1e-3 # uS
g_max_E2E_AMPA = 0.05 * 1e-3 / scale # uS
g_max_E2E_NMDA = 0.165 * 1e-3 / scale # uS
g_max_E2I_AMPA = 0.04 * 1e-3 / scale # uS
g_max_E2I_NMDA = 0.13 * 1e-3 / scale # uS
g_max_I2E_GABAa = 1.3 * 1e-3 / scale # uS
g_max_I2I_GABAa = 1.0 * 1e-3 / scale # uS
Build the network
[13]:
# E neurons/pyramid neurons
A = LIF(num_A, Cm=0.5, gL=0.025, t_refractory=2.)
B = LIF(num_B, Cm=0.5, gL=0.025, t_refractory=2.)
N = LIF(num_N, Cm=0.5, gL=0.025, t_refractory=2.)
# I neurons/interneurons
I = LIF(num_inh, Cm=0.2, gL=0.020, t_refractory=1.)
[14]:
IA = PoissonStim(num_A, freq_var=10., t_interval=50.,
freq_mean=mu0 + mu0 / 100. * coherence)
IB = PoissonStim(num_B, freq_var=10., t_interval=50.,
freq_mean=mu0 - mu0 / 100. * coherence)
[15]:
noise_A = PoissonNoise(num_A, freq=poisson_freq)
noise_B = PoissonNoise(num_B, freq=poisson_freq)
noise_N = PoissonNoise(num_N, freq=poisson_freq)
noise_I = PoissonNoise(num_inh, freq=poisson_freq)
[16]:
IA2A = AMPA_One(pre=IA, post=A, g_max=g_max_ext2E_AMPA)
IB2B = AMPA_One(pre=IB, post=B, g_max=g_max_ext2E_AMPA)
[17]:
## define E2E conn
A2A_AMPA = AMPA(pre=A, post=A, g_max=g_max_E2E_AMPA * w_pos)
A2A_NMDA = NMDA(pre=A, post=A, g_max=g_max_E2E_NMDA * w_pos)
A2B_AMPA = AMPA(pre=A, post=B, g_max=g_max_E2E_AMPA * w_neg)
A2B_NMDA = NMDA(pre=A, post=B, g_max=g_max_E2E_NMDA * w_neg)
A2N_AMPA = AMPA(pre=A, post=N, g_max=g_max_E2E_AMPA)
A2N_NMDA = NMDA(pre=A, post=N, g_max=g_max_E2E_NMDA)
B2A_AMPA = AMPA(pre=B, post=A, g_max=g_max_E2E_AMPA * w_neg)
B2A_NMDA = NMDA(pre=B, post=A, g_max=g_max_E2E_NMDA * w_neg)
B2B_AMPA = AMPA(pre=B, post=B, g_max=g_max_E2E_AMPA * w_pos)
B2B_NMDA = NMDA(pre=B, post=B, g_max=g_max_E2E_NMDA * w_pos)
B2N_AMPA = AMPA(pre=B, post=N, g_max=g_max_E2E_AMPA)
B2N_NMDA = NMDA(pre=B, post=N, g_max=g_max_E2E_NMDA)
N2A_AMPA = AMPA(pre=N, post=A, g_max=g_max_E2E_AMPA * w_neg)
N2A_NMDA = NMDA(pre=N, post=A, g_max=g_max_E2E_NMDA * w_neg)
N2B_AMPA = AMPA(pre=N, post=B, g_max=g_max_E2E_AMPA * w_neg)
N2B_NMDA = NMDA(pre=N, post=B, g_max=g_max_E2E_NMDA * w_neg)
N2N_AMPA = AMPA(pre=N, post=N, g_max=g_max_E2E_AMPA)
N2N_NMDA = NMDA(pre=N, post=N, g_max=g_max_E2E_NMDA)
## define E2I conn
A2I_AMPA = AMPA(pre=A, post=I, g_max=g_max_E2I_AMPA)
A2I_NMDA = NMDA(pre=A, post=I, g_max=g_max_E2I_NMDA)
B2I_AMPA = AMPA(pre=B, post=I, g_max=g_max_E2I_AMPA)
B2I_NMDA = NMDA(pre=B, post=I, g_max=g_max_E2I_NMDA)
N2I_AMPA = AMPA(pre=N, post=I, g_max=g_max_E2I_AMPA)
N2I_NMDA = NMDA(pre=N, post=I, g_max=g_max_E2I_NMDA)
I2A_GABAa = GABAa(pre=I, post=A, g_max=g_max_I2E_GABAa)
I2B_GABAa = GABAa(pre=I, post=B, g_max=g_max_I2E_GABAa)
I2N_GABAa = GABAa(pre=I, post=N, g_max=g_max_I2E_GABAa)
## define I2I conn
I2I_GABAa = GABAa(pre=I, post=I, g_max=g_max_I2I_GABAa)
## define external projections
noise2A = AMPA_One(pre=noise_A, post=A, g_max=g_max_ext2E_AMPA)
noise2B = AMPA_One(pre=noise_B, post=B, g_max=g_max_ext2E_AMPA)
noise2N = AMPA_One(pre=noise_N, post=N, g_max=g_max_ext2E_AMPA)
noise2I = AMPA_One(pre=noise_I, post=I, g_max=g_max_ext2I_AMPA)
[18]:
net = bp.Network(
# Synaptic Connections
noise2A, noise2B, noise2N, noise2I, IA2A, IB2B,
A2A_AMPA, A2A_NMDA, A2B_AMPA, A2B_NMDA, A2N_AMPA, A2N_NMDA, B2A_AMPA, B2A_NMDA,
B2B_AMPA, B2B_NMDA, B2N_AMPA, B2N_NMDA, N2A_AMPA, N2A_NMDA, N2B_AMPA, N2B_NMDA,
A2I_AMPA, A2I_NMDA, B2I_AMPA, B2I_NMDA, N2I_AMPA, N2I_NMDA, N2N_AMPA, N2N_NMDA,
I2A_GABAa, I2B_GABAa, I2N_GABAa, I2I_GABAa,
# Neuron Groups
noise_A, noise_B, noise_N, noise_I, N, I,
A=A, B=B, IA=IA, IB=IB,
monitors=['A.spike', 'B.spike', 'IA.freq', 'IB.freq']
)
[19]:
# build & simulate network
net.build()
ts = net.struct_run(total_period)
print(f'Used time: {ts} s')
Used time: 81.5979974269867 s
Visualization
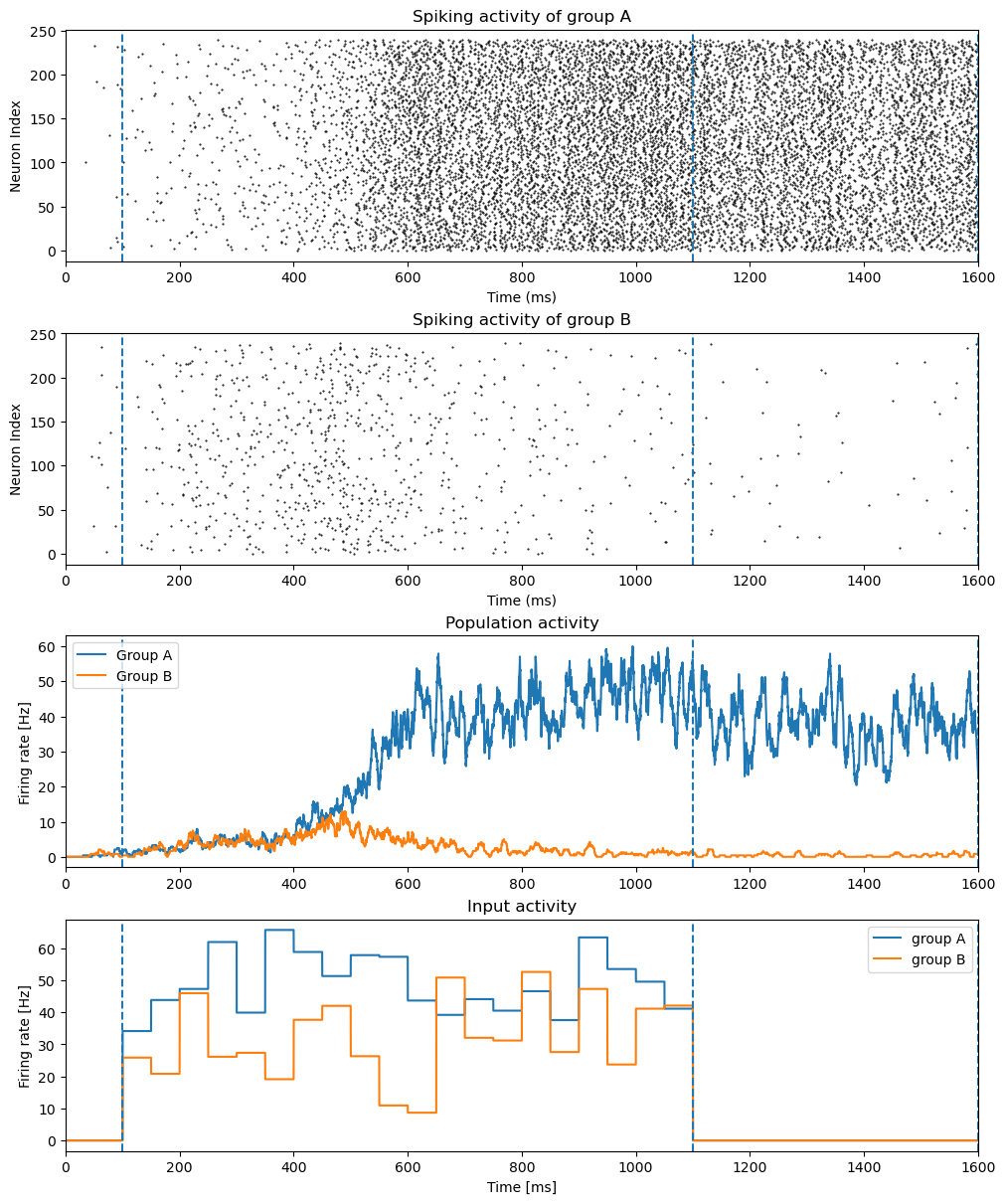
[20]:
fig, gs = bp.visualize.get_figure(4, 1, 3, 10)
t_start = 0.
fig.add_subplot(gs[0, 0])
bp.visualize.raster_plot(net.mon.ts, net.mon['A.spike'], markersize=1)
plt.title("Spiking activity of group A")
plt.ylabel("Neuron Index")
plt.xlim(t_start, total_period + 1)
plt.axvline(pre_period, linestyle='dashed')
plt.axvline(pre_period + stim_period, linestyle='dashed')
plt.axvline(pre_period + stim_period + delay_period, linestyle='dashed')
fig.add_subplot(gs[1, 0])
bp.visualize.raster_plot(net.mon.ts, net.mon['B.spike'], markersize=1)
plt.title("Spiking activity of group B")
plt.ylabel("Neuron Index")
plt.xlim(t_start, total_period + 1)
plt.axvline(pre_period, linestyle='dashed')
plt.axvline(pre_period + stim_period, linestyle='dashed')
plt.axvline(pre_period + stim_period + delay_period, linestyle='dashed')
fig.add_subplot(gs[2, 0])
rateA = bp.measure.firing_rate(net.mon['A.spike'], width=10.)
rateB = bp.measure.firing_rate(net.mon['B.spike'], width=10.)
plt.plot(net.mon.ts, rateA, label="Group A")
plt.plot(net.mon.ts, rateB, label="Group B")
plt.ylabel('Firing rate [Hz]')
plt.title("Population activity")
plt.xlim(t_start, total_period + 1)
plt.axvline(pre_period, linestyle='dashed')
plt.axvline(pre_period + stim_period, linestyle='dashed')
plt.axvline(pre_period + stim_period + delay_period, linestyle='dashed')
plt.legend()
fig.add_subplot(gs[3, 0])
plt.plot(net.mon.ts, net.mon['IA.freq'], label="group A")
plt.plot(net.mon.ts, net.mon['IB.freq'], label="group B")
plt.title("Input activity")
plt.ylabel("Firing rate [Hz]")
plt.xlim(t_start, total_period + 1)
plt.axvline(pre_period, linestyle='dashed')
plt.axvline(pre_period + stim_period, linestyle='dashed')
plt.axvline(pre_period + stim_period + delay_period, linestyle='dashed')
plt.legend()
plt.xlabel("Time [ms]")
plt.show()
