(Sussillo & Abbott, 2009) FORCE Learning
Implementation of the paper:
Sussillo, David, and Larry F. Abbott. “Generating coherent patterns of activity from chaotic neural networks.” Neuron 63, no. 4 (2009): 544-557.
[1]:
import numpy as np
import brainpy as bp
import brainpy.math.jax as bm
import matplotlib.pyplot as plt
[2]:
bp.math.use_backend('jax')
[3]:
class EchoStateNet(bp.DynamicalSystem):
r"""The continuous-time Echo State Network.
.. math::
\frac{dh}{dt} = -h + W_{ir} * x + W_{rr} * r + W_{or} * z \\
r = \tanh(h) \\
o = W_{ro} * r
"""
def __init__(self, num_input, num_hidden, num_output,
tau=1.0, dt=0.1, g=1.8, alpha=1.0, **kwargs):
super(EchoStateNet, self).__init__(**kwargs)
# parameters
self.num_input = num_input
self.num_hidden = num_hidden
self.num_output = num_output
self.tau = tau
self.dt = dt
self.g = g
self.alpha = alpha
# weights
self.w_ir = bm.random.normal(size=(num_input, num_hidden)) / bm.sqrt(num_input)
self.w_rr = g * bm.random.normal(size=(num_hidden, num_hidden)) / bm.sqrt(num_hidden)
self.w_or = bm.random.normal(size=(num_output, num_hidden))
w_ro = bm.random.normal(size=(num_hidden, num_output)) / bm.sqrt(num_hidden)
self.w_ro = bm.Variable(w_ro)
# variables
self.h = bm.Variable(bm.random.normal(size=num_hidden) * 0.5) # hidden
self.r = bm.tanh(self.h) # firing rate
self.o = bm.Variable(bm.dot(self.r, w_ro)) # output unit
self.P = bm.Variable(bm.eye(num_hidden) * self.alpha) # inverse correlation matrix
def update(self, x):
# update the hidden and output state
dhdt = -self.h + bm.dot(x, self.w_ir)
dhdt += bm.dot(self.r, self.w_rr)
dhdt += bm.dot(self.o, self.w_or)
self.h += self.dt / self.tau * dhdt
self.r.value = bm.tanh(self.h)
self.o.value = bm.dot(self.r, self.w_ro)
def rls(self, target):
# update the inverse correlation matrix
k = bm.expand_dims(bm.dot(self.P, self.r), axis=1) # (num_hidden, 1)
hPh = bm.dot(self.r.T, k) # (1,)
c = 1.0 / (1.0 + hPh) # (1,)
self.P -= bm.dot(k * c, k.T) # (num_hidden, num_hidden)
# update the output weights
e = bm.atleast_2d(self.o - target) # (1, num_output)
dw = bm.dot(-c * k, e) # (num_hidden, num_output)
self.w_ro += dw
def simulate(self, xs):
f = bm.make_loop(self.update, dyn_vars=[self.h, self.r, self.o], out_vars=[self.r, self.o])
return f(xs)
def train(self, xs, targets):
def _f(x):
input, target = x
self.update(input)
self.rls(target)
f = bm.make_loop(_f, dyn_vars=self.vars(), out_vars=[self.r, self.o])
return f([xs, targets])
[4]:
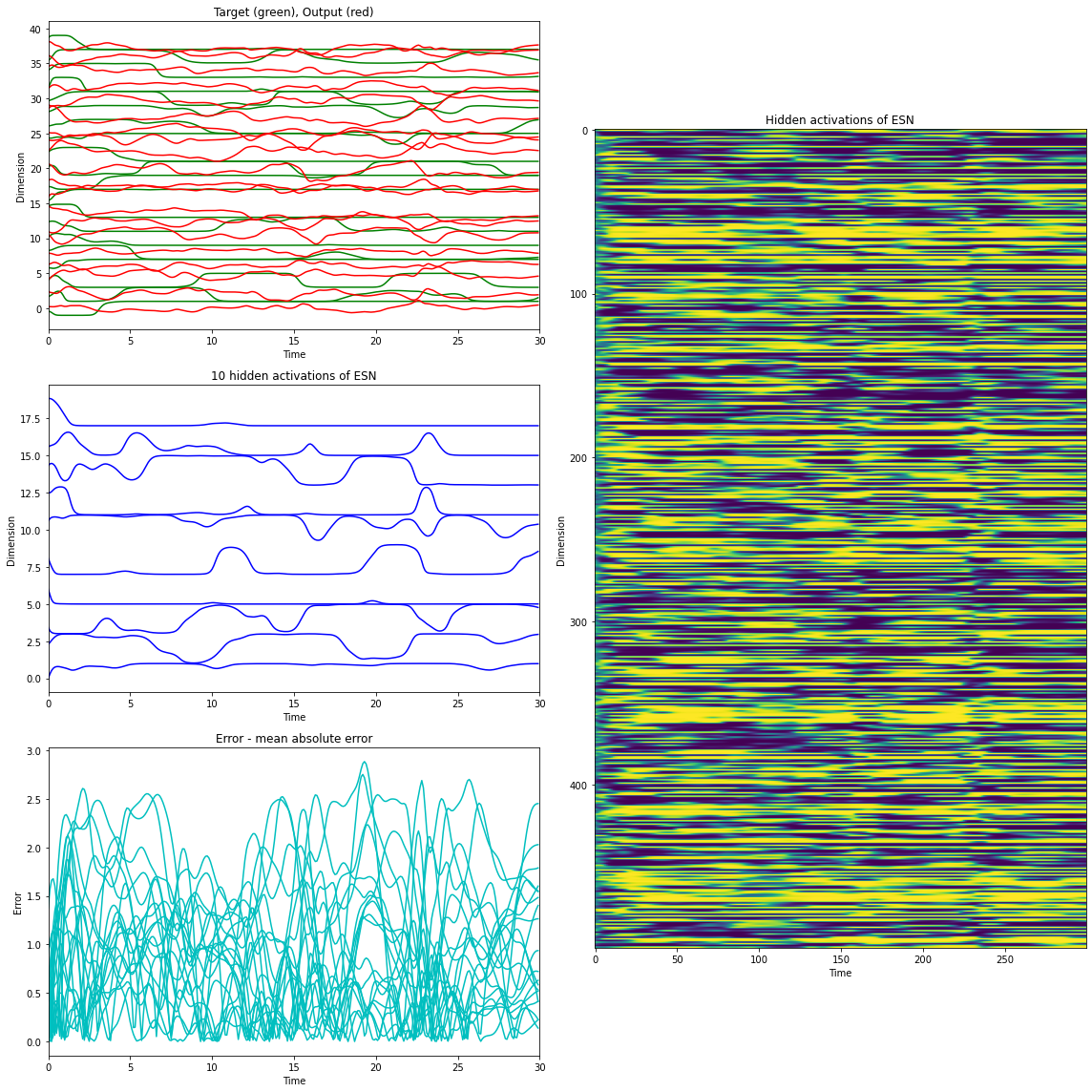
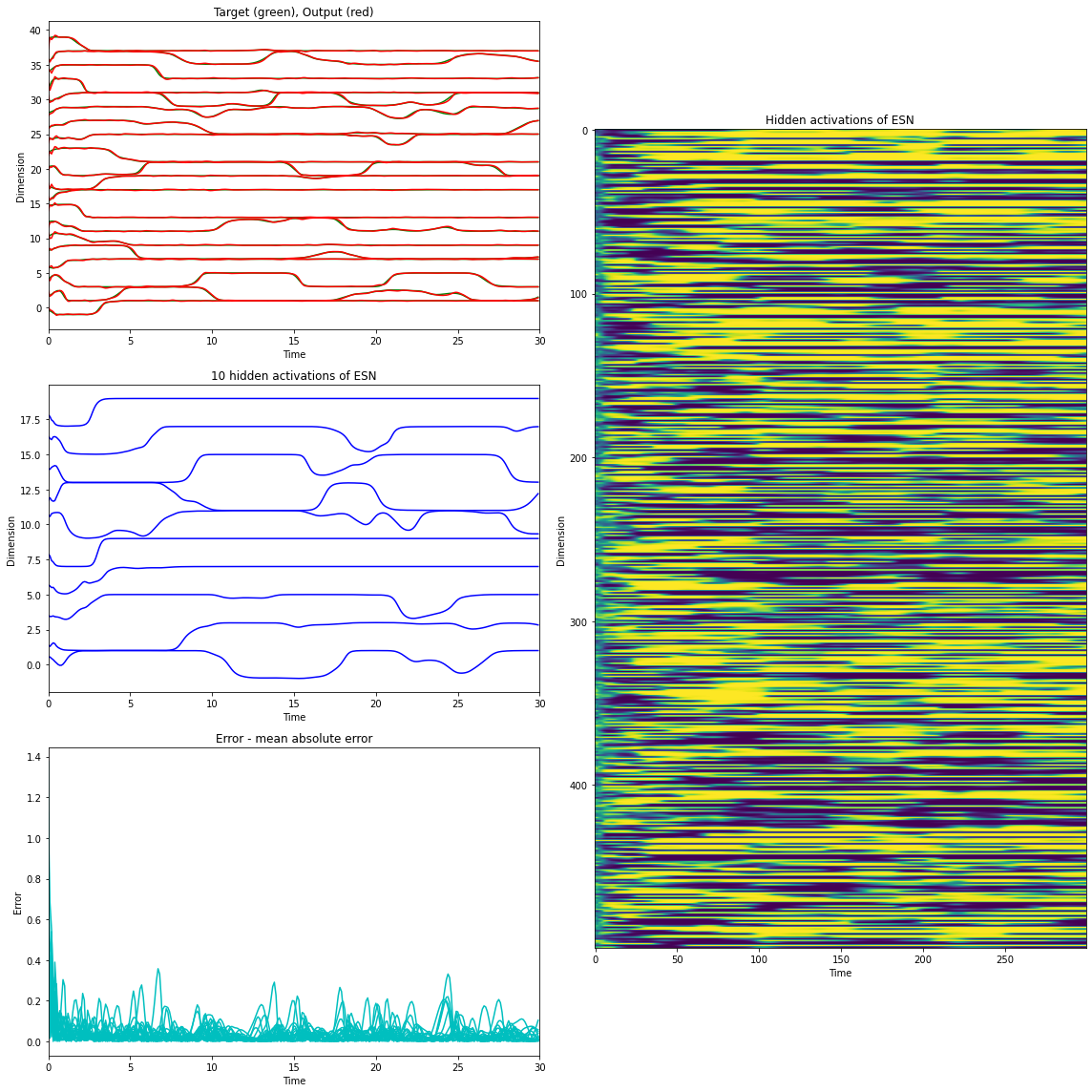
def print_force(ts, rates, outs, targets, duration, ntoplot=10):
"""Plot activations and outputs for the Echo state network."""
plt.figure(figsize=(16, 16))
plt.subplot(321)
plt.plot(ts, targets + 2 * np.arange(0, targets.shape[1]), 'g')
plt.plot(ts, outs + 2 * np.arange(0, outs.shape[1]), 'r')
plt.xlim((0, duration))
plt.title('Target (green), Output (red)')
plt.xlabel('Time')
plt.ylabel('Dimension')
plt.subplot(122)
plt.imshow(rates.T, interpolation=None)
plt.title('Hidden activations of ESN')
plt.xlabel('Time')
plt.ylabel('Dimension')
plt.subplot(323)
plt.plot(ts, rates[:, 0:ntoplot] + 2 * np.arange(0, ntoplot), 'b')
plt.xlim((0, duration))
plt.title('%d hidden activations of ESN' % (ntoplot))
plt.xlabel('Time')
plt.ylabel('Dimension')
plt.subplot(325)
plt.plot(ts, np.sqrt(np.square(outs - targets)), 'c')
plt.xlim((0, duration))
plt.title('Error - mean absolute error')
plt.xlabel('Time')
plt.ylabel('Error')
plt.tight_layout()
plt.show()
[5]:
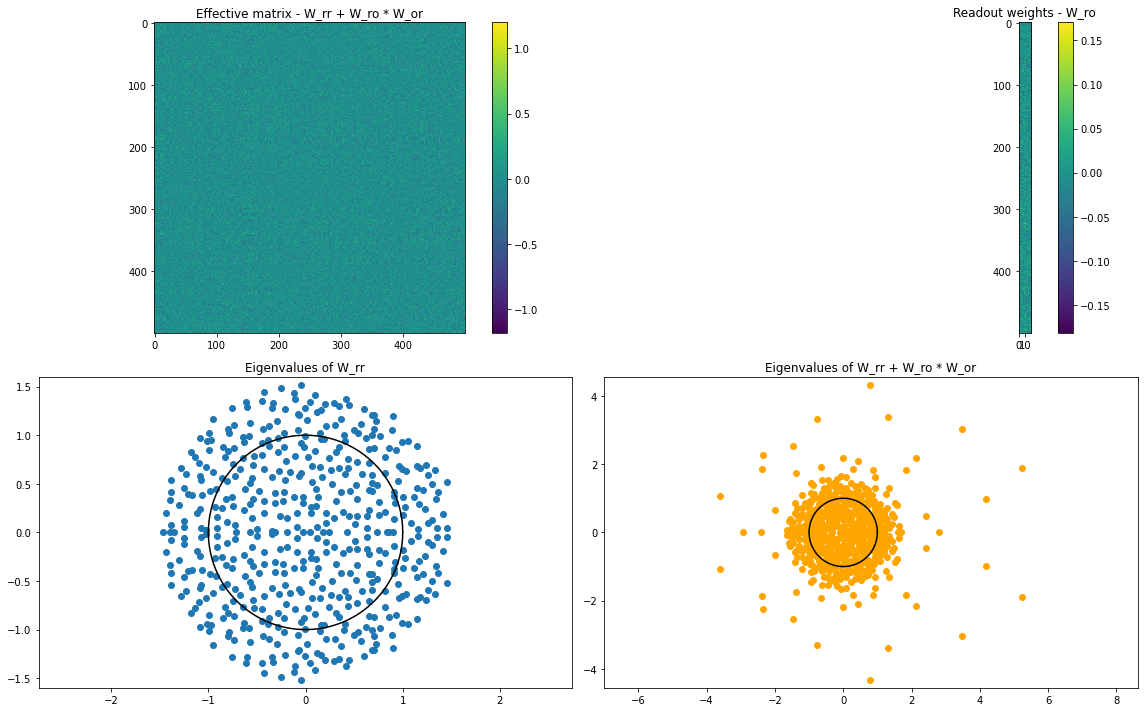
def plot_params(net):
"""Plot some of the parameters associated with the ESN."""
assert isinstance(net, EchoStateNet)
plt.figure(figsize=(16, 10))
plt.subplot(221)
plt.imshow((net.w_rr + net.w_ro @ net.w_or).numpy(), interpolation=None)
plt.colorbar()
plt.title('Effective matrix - W_rr + W_ro * W_or')
plt.subplot(222)
plt.imshow(net.w_ro.numpy(), interpolation=None)
plt.colorbar()
plt.title('Readout weights - W_ro')
x_circ = np.linspace(-1, 1, 1000)
y_circ = np.sqrt(1 - x_circ ** 2)
evals, _ = np.linalg.eig(net.w_rr.numpy())
plt.subplot(223)
plt.plot(np.real(evals), np.imag(evals), 'o')
plt.plot(x_circ, y_circ, 'k')
plt.plot(x_circ, -y_circ, 'k')
plt.axis('equal')
plt.title('Eigenvalues of W_rr')
evals, _ = np.linalg.eig((net.w_rr + net.w_ro @ net.w_or).numpy())
plt.subplot(224)
plt.plot(np.real(evals), np.imag(evals), 'o', color='orange')
plt.plot(x_circ, y_circ, 'k')
plt.plot(x_circ, -y_circ, 'k')
plt.axis('equal')
plt.title('Eigenvalues of W_rr + W_ro * W_or')
plt.tight_layout()
plt.show()
[6]:
dt = 0.1
T = 30
times = bm.arange(0, T, dt)
xs = bm.zeros((times.shape[0], 1))
Generate some target data by running an ESN, and just grabbing hidden dimensions as the targets of the FORCE trained network.
[7]:
esn1 = EchoStateNet(num_input=1, num_hidden=500, num_output=20, dt=dt, g=1.8)
rs, ys = esn1.simulate(xs)
targets = rs[:, 0: esn1.num_output] # This will be the training data for the trained ESN
plt.plot(times, targets + 2 * np.arange(0, esn1.num_output), 'g')
plt.xlim((0, T))
plt.ylabel('Dimensions')
plt.xlabel('Time')
plt.show()

Un-trained ESN.
[8]:
esn2 = EchoStateNet(num_input=1, num_hidden=500, num_output=20, dt=dt, g=1.5)
rs, ys = esn2.simulate(xs) # the untrained ESN
print_force(times, rates=rs, outs=ys, targets=targets, duration=T, ntoplot=10)
Trained ESN.
[9]:
esn3 = EchoStateNet(num_input=1, num_hidden=500, num_output=20, dt=dt, g=1.5, alpha=1.)
rs, ys = esn3.train(xs=xs, targets=targets) # train once
print_force(times, rates=rs, outs=ys, targets=targets, duration=T, ntoplot=10)
[10]:
plot_params(esn3)